„Apertúra antennák” változatai közötti eltérés
(Lencse antennák - Fresnel számítások) |
a (formázás) |
||
| (7 közbenső módosítás ugyanattól a szerkesztőtől nincs mutatva) | |||
| 5. sor: | 5. sor: | ||
* rövidhullámon igen elterjedt az antennanyereség viszonyítási alapját adó [[dipól]] antenna, amely ezáltal 0 [[dBd]] nyereségű. Továbbá a hurokantennák jelentősek. | * rövidhullámon igen elterjedt az antennanyereség viszonyítási alapját adó [[dipól]] antenna, amely ezáltal 0 [[dBd]] nyereségű. Továbbá a hurokantennák jelentősek. | ||
* ultrarövid hullámú sávban a [[Yagi]] és a többelemes [[Quad]]. | * ultrarövid hullámú sávban a [[Yagi]] és a többelemes [[Quad]]. | ||
| − | * a mikrohullámú sáv felé átveszi az uralmat a parabolatükör, a mikrostrip antenna, de a frekvencia növekedtével a lencsés fókuszálás is egyre inkább képbe kerülhet. | + | * a mikrohullámú sáv felé átveszi az uralmat a parabolatükör, a [[mikrostrip antenna]], de a frekvencia növekedtével a lencsés fókuszálás is egyre inkább képbe kerülhet. |
Többek között azért váltják fel a Yagi antennát az apertúra antennák, mert szeretnénk nagyobb nyereségű antennát, és | Többek között azért váltják fel a Yagi antennát az apertúra antennák, mert szeretnénk nagyobb nyereségű antennát, és | ||
* a Yagi antenna hosszának növelése nem hoz jelentős nyereségnövekedést, például 7 lambda hosszúság 16 dBd | * a Yagi antenna hosszának növelése nem hoz jelentős nyereségnövekedést, például 7 lambda hosszúság 16 dBd | ||
| − | * csoportantenna elrendezéssel ugyan tudunk nyereséget növelni, de egy 4x4-es (16 Yagis) csoporttal sem | + | * [[csoportantenna]] elrendezéssel ugyan tudunk nyereséget növelni, de egy 4x4-es (16 Yagis) csoporttal sem haladjuk meg a 25-30 dBd nyereséget |
* ezzel szemben egy 10 lambda átmérőjű tükör, fókuszában egy dipóllal egyszerű felépítése ellenére is eléri ezt a nyereséget. | * ezzel szemben egy 10 lambda átmérőjű tükör, fókuszában egy dipóllal egyszerű felépítése ellenére is eléri ezt a nyereséget. | ||
| 60. sor: | 60. sor: | ||
A gyakorlatban alkalmazható visszaverő anyagok 2-3 dB-lel rontják ezt az értéket. | A gyakorlatban alkalmazható visszaverő anyagok 2-3 dB-lel rontják ezt az értéket. | ||
| − | Egy másik megfogalmazásban, amely a visszaverőképesség 2 dB-jét is beleszámítja: <math>G_{dBi} = 17,82 + 20 \cdot lg D + 20 \cdot lg F[GHz]</math> | + | <szamolo sor=4 oszlop=36 szoveg="D: méter, F: GHz" jobb>D = 0.8;F = 1.2;;G_dBi=17.82+20*log10(D)+20*log10(F);</szamolo> |
| + | Egy másik megfogalmazásban, amely a visszaverőképesség 2 dB-jét is beleszámítja: | ||
| + | |||
| + | <math>G_{dBi} = 17,82 + 20 \cdot lg D + 20 \cdot lg F[GHz]</math> | ||
ahol: | ahol: | ||
| 71. sor: | 74. sor: | ||
{| align="right" | {| align="right" | ||
| − | | [[Kép:Parabola cassegrain.jpg|thumb|Cassegrain antenna]] || [[Kép:Offset parabola.jpg|thumb| | + | | [[Kép:Parabola cassegrain.jpg|thumb|Cassegrain antenna]] || [[Kép:Offset parabola.jpg|thumb|Off-set parabola]] |
|} | |} | ||
Említésre méltó trükk a Cassegrain antenna, amelynél a pontszerű sugárzó képzeletbeli helye és a reflektor között egy hiperbola alakú segédreflektor található. A sugárforrás ekkor a paraboloid síkjába hátratolható. Bonyolultsága miatt csak indokolt esetben alkalmazzák. | Említésre méltó trükk a Cassegrain antenna, amelynél a pontszerű sugárzó képzeletbeli helye és a reflektor között egy hiperbola alakú segédreflektor található. A sugárforrás ekkor a paraboloid síkjába hátratolható. Bonyolultsága miatt csak indokolt esetben alkalmazzák. | ||
| − | A másik trükk az | + | A másik trükk az off-set parabola, amellyel igen gyakran találkozhatunk. Nevéből is adódik, hogy a sugárzó kívülre van állítva (off-set) a sugárnyalábból. Ennek lényege, hogy a parabola ívet egyik irányban dolgozzák ki nagyobb x érték felé, a másik irányban kevésbé. A sugárforrást pedig nem az x=0 pontra irányítják, hanem attól a kidolgozott oldal felé. |
Enek a megoldásnak több előnye is van: | Enek a megoldásnak több előnye is van: | ||
* a sugárforrás nem lóg bele a tükör által visszavert nyalábba | * a sugárforrás nem lóg bele a tükör által visszavert nyalábba | ||
| − | * műholdvételkor nem az ég felé áll az antenna tükre | + | * műholdvételkor nem az ég felé áll az antenna tükre, hanem közel függőlegesen, és a sugárzó alul van elhelyeve egy rövid merevítőkaron. |
| + | * ezáltal a műhold felé fordított antennában nem áll meg a csapadék. (Ne feledjük, egyenlítő felé közeledve erőteljesebben vannak az ég felé fordítva) | ||
| + | |||
| + | Hátrányáról se feledkezzünk meg: | ||
| + | * állítólag a keresztpolarizációs elnyomása éppen az asszimmetriája miatt gyengébb. | ||
| + | |||
| + | Távközlési paraboláknál találkozhatunk dob antennával. A dob RF szempontból egy árnyékoló gallér a parabola tükör előtt. Kimutatták, hogy a gallér alkalmazásával a sugárzási iránytól eltérő irányból érkező idegen zavaró jelekre erőteljesebb elnyomást biztosít. | ||
=== Fotók === | === Fotók === | ||
| 86. sor: | 95. sor: | ||
{| | {| | ||
| [[Kép:Parabola antenna.jpg | thumb | „klasszikus” parabola]] | | [[Kép:Parabola antenna.jpg | thumb | „klasszikus” parabola]] | ||
| − | | [[Kép:Offset parabola2.jpg | thumb | | + | | [[Kép:Offset parabola2.jpg | thumb | Off-set parabola]] |
| [[Kép:Parabola cassegrain2.jpg | thumb | Cassegrain parabola]] | | [[Kép:Parabola cassegrain2.jpg | thumb | Cassegrain parabola]] | ||
|- | |- | ||
| 122. sor: | 131. sor: | ||
|} | |} | ||
| − | + | Legyen ''f'' a fókusztávolság. Ekkor a gyűrűk kezdete és vége az alábbi képletből meghatározható: <math>r_n = \sqrt{2 n \lambda F} = \sqrt{\frac{0,6 \cdot F}{f[GHz]} \cdot n}</math> | |
| − | |||
| − | Legyen ''f'' a fókusztávolság. Ekkor a gyűrűk kezdete és vége az alábbi képletből meghatározható: <math>r_n = \sqrt{2 n \lambda F}</math> | ||
ahol: | ahol: | ||
* r<sub>n</sub>: az n-edik gyűrűváltozás távolsága a középpontól (méter). A gyűrű az egyik változástól a másik változásig tart, majd szünet és utána ismét gyűrű. | * r<sub>n</sub>: az n-edik gyűrűváltozás távolsága a középpontól (méter). A gyűrű az egyik változástól a másik változásig tart, majd szünet és utána ismét gyűrű. | ||
| − | * n: index, 1 ... N-ig. | + | * n: index, 1 ... N-ig (N páros pozitív egész szám, ennek fele lesz a gyűrűszám). |
* λ: hullámhossz méterben | * λ: hullámhossz méterben | ||
* F: fókusztávolság méterben | * F: fókusztávolság méterben | ||
| + | * f: frekvencia GHz-ben megadva | ||
| + | |||
| + | A Fresnel-lencse nyeresége: G = 20 * lg(gyűrűszám). | ||
Egy-két próbaszámítás után belátható, hogy a Fresnel-zónás lencsék szintén mikrohullámon nyújtanak izgalmas megoldást. | Egy-két próbaszámítás után belátható, hogy a Fresnel-zónás lencsék szintén mikrohullámon nyújtanak izgalmas megoldást. | ||
[[Kategória:Antennák]] | [[Kategória:Antennák]] | ||
A lap jelenlegi, 2011. február 6., 10:27-kori változata
Tartalomjegyzék
Bevezető
A rádióamatőr gyakorlatban a hullámhossz szerint választunk különböző nyereségű antennákat.
- hosszúhullámon örülünk, ha sugároz a hullámhossz töredékméretében implementált tekercsantennánk.
- rövidhullámon igen elterjedt az antennanyereség viszonyítási alapját adó dipól antenna, amely ezáltal 0 dBd nyereségű. Továbbá a hurokantennák jelentősek.
- ultrarövid hullámú sávban a Yagi és a többelemes Quad.
- a mikrohullámú sáv felé átveszi az uralmat a parabolatükör, a mikrostrip antenna, de a frekvencia növekedtével a lencsés fókuszálás is egyre inkább képbe kerülhet.
Többek között azért váltják fel a Yagi antennát az apertúra antennák, mert szeretnénk nagyobb nyereségű antennát, és
- a Yagi antenna hosszának növelése nem hoz jelentős nyereségnövekedést, például 7 lambda hosszúság 16 dBd
- csoportantenna elrendezéssel ugyan tudunk nyereséget növelni, de egy 4x4-es (16 Yagis) csoporttal sem haladjuk meg a 25-30 dBd nyereséget
- ezzel szemben egy 10 lambda átmérőjű tükör, fókuszában egy dipóllal egyszerű felépítése ellenére is eléri ezt a nyereséget.
Ezért a hullámhossz csökkenésével, illetve a rádióamatőr elszántságával arányban nagyobb hullámhosszon is előfordulhat, hogy Fresnel lencsés vagy reflektorfalas antenna (például parabolaantenna) lesz alkalmazva. Alább ezeket az antennatípusok kerülnek bemutatásra.
Parabola antenna
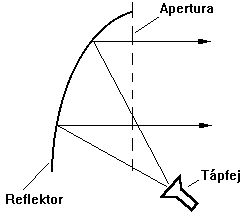
A síkparabola, mint alakzat jellegzetes tulajdonsága, hogy a fókuszpontjából a síkparabola bármely pontjára húzunk képzeletben egy vonalat, az onnan történő visszatükröződés nemcsak hogy párhuzamos irányokat eredményet, de fázisban is pontosan azonos fázisú hullámfrontot.
A síkparabola kiszámítása: [math]y = \frac{x^2}{4 F}[/math]
ahol:
- x: elfeltetett parabola vízszintes irányban (+/- irányban, azaz jobbra és balra)
- y: függőleges irányban
- F: kívánt fókusztávolság (magasság) az x=0 pontban
Például: ha szeretnénk egy olyan parabolát szerkeszteni, amelynél a sugárzót 0,4 méternyire szeretnénk előrehozni, akkor y = x2 / (4 F) = x2 / (4 * 0.4) = x2 / (1,6). Továbbá egy másik példa is bemutatásra kerül, ahol 0,8 méternyire toljuk előre a sugárzót (F = 0.8 m)
Az alábbi táblázatban a 0 a középpont, tőle balra és jobbra a táblázatban foglalt távolsággal emelkednek ki a tükrőző elemek.
| x (bal, jobb): | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 méter |
| y (F = 0.4m): | 0 | 6,25 | 25 | 56,25 | 100 | 156 | 225 | 306 | 400 | 506 | 625 | 756 | 900 | 1056 | 1225 | 1406 | 1600 | 1806 mm |
| y (F = 0.8m): | 0 | 3.12 | 12.5 | 28.12 | 50 | 78 | 112.5 | 153 | 200 | 253 | 312 | 378 | 450 | 528 | 612 | 703 | 800 | 903 mm |
És természetesen a köztes értékek is kiszámolhatók. Illetve a parabolát akkora méretig számítjuk, amekkorát szeretnénk építeni.
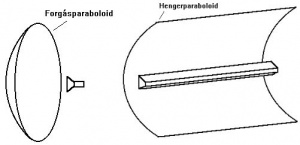
Forgásparaboloid és hengerparaboloid
A térbeli parabolákat paraboloidoknak hívják. Megkülönböztetünk forgásparaboloidot és hengerparaboloidot. Az ábrán szembetűnik rögtön a különbség. A forágásparaboloid horizontálisan és vertilálisan is szűkíti a nyalábot, míg a hengerparaboloid csak a parabola síkjában szűkíti a sugárzott nyalábot.
Gyakorlatban azonban a kettő között még egy különbség van. A forgásparaboloid pontszerű sugárzót feltételez. Azaz a sugárzó mérete elhanyagolható a paraboloid méretéhez képest.
Ezzel szemben a hengerparaboloid hengeres síkjában elhelyezhető például egy nagyobb kiterjedésű dipól sugárzóelem.
Egy 100% reflexióképességű anyagból készült forgásparaboloid antenna elvi nyeresége: [math]G_{dBi} = 20 \cdot lg \frac{ \pi \cdot D}{\lambda} = 10 \cdot lg \frac{4 \pi \cdot A}{\lambda^2}[/math]
ahol:
- D a tükör átmérője méterben
- λ: hullámhossz méterben
- A: tükör felülete négyzetméterben
A gyakorlatban alkalmazható visszaverő anyagok 2-3 dB-lel rontják ezt az értéket.
<szamolo sor=4 oszlop=36 szoveg="D: méter, F: GHz" jobb>D = 0.8;F = 1.2;;G_dBi=17.82+20*log10(D)+20*log10(F);</szamolo> Egy másik megfogalmazásban, amely a visszaverőképesség 2 dB-jét is beleszámítja:
[math]G_{dBi} = 17,82 + 20 \cdot lg D + 20 \cdot lg F[GHz][/math]
ahol:
- D a tükör átmérője méterben
- F a frekvencia GHz-ben megadva
A forgásparaboloid nyílásszöge a -3 dB-es pontok között: [math]\Delta\varphi=\frac{21,3}{D \cdot F[GHz]}[/math]
Egyéb trükkök
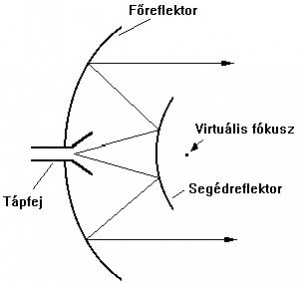
Említésre méltó trükk a Cassegrain antenna, amelynél a pontszerű sugárzó képzeletbeli helye és a reflektor között egy hiperbola alakú segédreflektor található. A sugárforrás ekkor a paraboloid síkjába hátratolható. Bonyolultsága miatt csak indokolt esetben alkalmazzák.
A másik trükk az off-set parabola, amellyel igen gyakran találkozhatunk. Nevéből is adódik, hogy a sugárzó kívülre van állítva (off-set) a sugárnyalábból. Ennek lényege, hogy a parabola ívet egyik irányban dolgozzák ki nagyobb x érték felé, a másik irányban kevésbé. A sugárforrást pedig nem az x=0 pontra irányítják, hanem attól a kidolgozott oldal felé.
Enek a megoldásnak több előnye is van:
- a sugárforrás nem lóg bele a tükör által visszavert nyalábba
- műholdvételkor nem az ég felé áll az antenna tükre, hanem közel függőlegesen, és a sugárzó alul van elhelyeve egy rövid merevítőkaron.
- ezáltal a műhold felé fordított antennában nem áll meg a csapadék. (Ne feledjük, egyenlítő felé közeledve erőteljesebben vannak az ég felé fordítva)
Hátrányáról se feledkezzünk meg:
- állítólag a keresztpolarizációs elnyomása éppen az asszimmetriája miatt gyengébb.
Távközlési paraboláknál találkozhatunk dob antennával. A dob RF szempontból egy árnyékoló gallér a parabola tükör előtt. Kimutatták, hogy a gallér alkalmazásával a sugárzási iránytól eltérő irányból érkező idegen zavaró jelekre erőteljesebb elnyomást biztosít.
Fotók
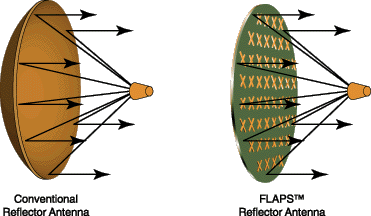
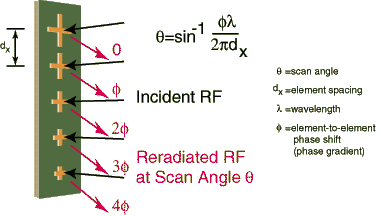
Lapos apertúra antenna (Flaps antenna)
Ez egy érdekes antenna típus. A lényege, hogy a sugárzó egy sík hátlapra irányítja anyalábját, ahol apró rezonáns elemek módosítják, és a módosítás hatására érik el a sugárzás koncentrálását. Hogy megértsük a működését, egysorban megépített elrendezést vázol a másik ábra.
Ezt az antennatípust ne tévesszük össze a microstrip antennával, utóbbi esetén ugyanis a NYÁK-on van kialakítva sok sugárzóból és tápvonalakból egy a dipólfüggöny antennához hasonló elven működő csoportantenna.
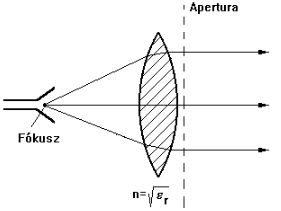
Lencse antennák
Nagyobb frekvenciákon - egészen a fényig, igen izgalmas téma a lencsével történő hatásos felület növelés. A lencse hallatán mindenki először az optikai üveglencsére, netán az étkezési lencsére gondol. Mikrohullám esetén azonban van még egy izgalmas megoldásra lehetőség: a Fresnel-lencsék alkalmazhatósága. A Fresnel lencséket kétféleképp lehet használni:
- az ábrán látható, dielektrikum lépcsős marásával kialakított fáziskorrekciót végző elem módszerével
- a résen való elhajlást kiaknázó megoldással. Ekkor a lencse bizonyos távolságokra elhelyetett fémlemezek segítségével lesz megvalósítva.
Legyen f a fókusztávolság. Ekkor a gyűrűk kezdete és vége az alábbi képletből meghatározható: [math]r_n = \sqrt{2 n \lambda F} = \sqrt{\frac{0,6 \cdot F}{f[GHz]} \cdot n}[/math]
ahol:
- rn: az n-edik gyűrűváltozás távolsága a középpontól (méter). A gyűrű az egyik változástól a másik változásig tart, majd szünet és utána ismét gyűrű.
- n: index, 1 ... N-ig (N páros pozitív egész szám, ennek fele lesz a gyűrűszám).
- λ: hullámhossz méterben
- F: fókusztávolság méterben
- f: frekvencia GHz-ben megadva
A Fresnel-lencse nyeresége: G = 20 * lg(gyűrűszám).
Egy-két próbaszámítás után belátható, hogy a Fresnel-zónás lencsék szintén mikrohullámon nyújtanak izgalmas megoldást.