„Induktivitás” változatai közötti eltérés
a (Az induktivitás feladata - hivatkozások) |
a (URL frissítés) |
||
| (3 közbenső módosítás, amit 2 másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | == Az induktivitás | + | == Az induktivitás áramköri szerepe == |
* [[aluláteresztő szűrő]] (LC vagy RL) induktivitásaként - zavarszűrés (illetve ''tüske'' elnyomás) | * [[aluláteresztő szűrő]] (LC vagy RL) induktivitásaként - zavarszűrés (illetve ''tüske'' elnyomás) | ||
* kondenzátorral összekapcsolva sávszűrő (LC szűrő, [[rezgőkör]]) | * kondenzátorral összekapcsolva sávszűrő (LC szűrő, [[rezgőkör]]) | ||
* a mágneses tér összeomlasztásán alapuló feszültségcsökkentő illetve feszültségnövelő kapcsolás fojtója | * a mágneses tér összeomlasztásán alapuló feszültségcsökkentő illetve feszültségnövelő kapcsolás fojtója | ||
| + | |||
| + | ''Figyelem'': az induktivitás nem csak mint elemi alkatrész van jelen az elektronikában, hanem bármely vezető két pontja között úgynevezett szórt induktivitás mérhető. Szerencsére az egyenes vezetőnek kicsi az induktivitása, de nagyfrekvencián nem elhanyagolható. | ||
== Az induktivitás fogalma == | == Az induktivitás fogalma == | ||
| − | Az induktivitás mértékegysége a '' | + | Az induktivitás mértékegysége a ''henry'', jele ''H''. Rádiótechnikában leggyakrabban a nH, µH és mH nagyságrendbe eső tekercsekkel találkozunk. Az induktivitáson (köznapi nevén tekercsen) átfolyó áram létrehoz a tekercs körül egy mágneses teret, amely mágneses tér változása ellentétesen hat az áram növekedésére. Azaz ha tekercsre egy feszültségforrást kapcsolunk, a rajta átfolyó áram nem ugrásszerűen jön létre, hanem folyamatosan növekszik. A áram növekedésének korlátozódása a tekercs induktivitása. Azaz: |
<szamolo sor=5 oszlop=15 jobb>U = 4,5;L = 100 milli;t = 0,01;;I = U/L * t;</szamolo> | <szamolo sor=5 oszlop=15 jobb>U = 4,5;L = 100 milli;t = 0,01;;I = U/L * t;</szamolo> | ||
| 46. sor: | 48. sor: | ||
A induktivitás hátteréről bővebben a [[mágneses mező]] című fejezetben olvashatunk. | A induktivitás hátteréről bővebben a [[mágneses mező]] című fejezetben olvashatunk. | ||
| − | * Induktivitást fajlagos induktivitásból és menetszámból [ | + | * Induktivitást fajlagos induktivitásból és menetszámból [https://hg9ieg.hu/szamolo/_sz/L_ALN.html számoló]. |
| − | * Menetszámot fajlagos induktivitásból és induktivitásból [ | + | * Menetszámot fajlagos induktivitásból és induktivitásból [https://hg9ieg.hu/szamolo/_sz/N_ALL.html számoló]. |
| − | * Fajlagos induktivitást induktivitásból és menetszámból [ | + | * Fajlagos induktivitást induktivitásból és menetszámból [https://hg9ieg.hu/szamolo/_sz/AL_LN.html számoló]. |
== Az induktivitás egyenáramú körben == | == Az induktivitás egyenáramú körben == | ||
| 58. sor: | 60. sor: | ||
;ahol: | ;ahol: | ||
| − | *''L'' az induktivitás, | + | *''L'' az induktivitás, [L] = henry = H, |
| − | *''U'' a feszültség, | + | *''U'' a feszültség, [U] = volt = V, |
| − | *''t'' a feszültség rákapcsolásának ideje | + | *''t'' a feszültség rákapcsolásának ideje, [t] = másodperc = s. |
'''Megjegyzés:''' a gyakorlatban csak rövid ''t'' időre kapcsoljunk a tekercs sarkaira feszültséget, majd kapcsoljuk le róla. Ellenkező esetben a kialakuló nagy áramerősség tönkreteheti a tekercset is és a tápforrást is rövidzárral terhelheti. Egyébként a [[kapcsolóüzemű tápegység]]eknél figyelhető meg ennek a jelenségnek a gyakorlati alkalmazása. | '''Megjegyzés:''' a gyakorlatban csak rövid ''t'' időre kapcsoljunk a tekercs sarkaira feszültséget, majd kapcsoljuk le róla. Ellenkező esetben a kialakuló nagy áramerősség tönkreteheti a tekercset is és a tápforrást is rövidzárral terhelheti. Egyébként a [[kapcsolóüzemű tápegység]]eknél figyelhető meg ennek a jelenségnek a gyakorlati alkalmazása. | ||
A tekercsben tárolt energia: <math>E=\frac{1}{2} L I^2</math>. | A tekercsben tárolt energia: <math>E=\frac{1}{2} L I^2</math>. | ||
| + | |||
| + | * [E] = joule = J. | ||
| + | * [I] = amper = A. | ||
| + | |||
| + | A <math>\Psi = I \cdot L\,</math> [[mágneses fluxus|tekercsfluxust]] használva <math>E = \frac{1}{2} \cdot \frac{\Psi^2}{L}\,</math>. | ||
| + | |||
| + | * [Ψ] = weber = Wb. | ||
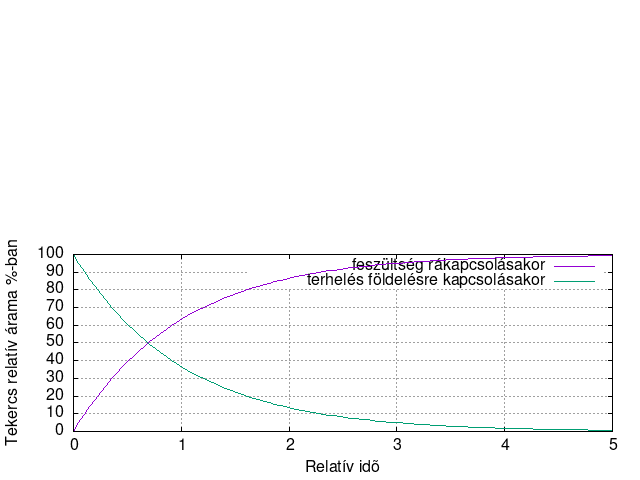
Tekintettel arra, hogy a rézhuzalból készült tekercsnek van ohmos ellenállása, nézzük meg, hogyan alakul a tekercs időbeli árama, ha rákapcsolunk egy adott feszültségű tápegységet illetve ha átkapcsoljuk a gerjesztett állapotú tekercset egy R értékű terhelőellenálláson a föld felé. | Tekintettel arra, hogy a rézhuzalból készült tekercsnek van ohmos ellenállása, nézzük meg, hogyan alakul a tekercs időbeli árama, ha rákapcsolunk egy adott feszültségű tápegységet illetve ha átkapcsoljuk a gerjesztett állapotú tekercset egy R értékű terhelőellenálláson a föld felé. | ||
| 87. sor: | 96. sor: | ||
A τ érték azért fontos, mert 1 τ idő alatt (τ = L/R) egy induktivitás a rákapcsolt feszültség hatására a maximális áramának 63%-át folyatja már át illetve amikor egy gerjesztett állapotban levő tekercset a kisütőellenállásra kapcsolunk, akkor 37%-ára esik τ idő alatt vissza. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-át éri el gerjesztéskor az áram, illetve kisütése esetén 5 τ idő alatt már csak 0,7 % marad a tekercsben. Tehát 5 τ idő alatt egy tekercs gyakorlatilag teljesen elveszti a tárolt energiáját. | A τ érték azért fontos, mert 1 τ idő alatt (τ = L/R) egy induktivitás a rákapcsolt feszültség hatására a maximális áramának 63%-át folyatja már át illetve amikor egy gerjesztett állapotban levő tekercset a kisütőellenállásra kapcsolunk, akkor 37%-ára esik τ idő alatt vissza. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-át éri el gerjesztéskor az áram, illetve kisütése esetén 5 τ idő alatt már csak 0,7 % marad a tekercsben. Tehát 5 τ idő alatt egy tekercs gyakorlatilag teljesen elveszti a tárolt energiáját. | ||
| + | |||
| + | * Energiát áramerősségből és induktivitásból [https://hg9ieg.hu/szamolo/_sz/EPsi_IL.html számoló] | ||
| + | * Áramerősséget energiából és induktivitásból [https://hg9ieg.hu/szamolo/_sz/IPsi_EL.html számoló] | ||
| + | * Induktivitást energiából és áramerősségből [https://hg9ieg.hu/szamolo/_sz/LPsi_EI.html számoló] | ||
| + | * Induktivitást ellenállásból és időállandóból [https://hg9ieg.hu/szamolo/_sz/CL_Rtau.html számoló] | ||
| + | * Ellenállást induktivitásból és időállandóból [https://hg9ieg.hu/szamolo/_sz/CR_Ltau.html számoló] | ||
| + | * Időállandót induktivitásból és ellenállásból [https://hg9ieg.hu/szamolo/_sz/Ctau_LR.html számoló] | ||
== Az induktivitás váltakozóáramú körben == | == Az induktivitás váltakozóáramú körben == | ||
| 102. sor: | 118. sor: | ||
Impedancia: <math>Z = j X_L = j 2\pi \cdot f \cdot L [ \Omega ]</math>. | Impedancia: <math>Z = j X_L = j 2\pi \cdot f \cdot L [ \Omega ]</math>. | ||
| − | * Látszólagos ellenállást és impedanciát frekvenciából és induktivitásból [ | + | * Látszólagos ellenállást és impedanciát frekvenciából és induktivitásból [https://hg9ieg.hu/szamolo/_sz/YZ_fL.html számoló]. |
| − | * Induktivitást frekvenciából és látszólagos ellenállásból vagy impedanciából [ | + | * Induktivitást frekvenciából és látszólagos ellenállásból vagy impedanciából [https://hg9ieg.hu/szamolo/_sz/L_fZ.html számoló]. |
| − | * Frekvenciát induktivitásból és látszólagos ellenállásból vagy impedanciából [ | + | * Frekvenciát induktivitásból és látszólagos ellenállásból vagy impedanciából [https://hg9ieg.hu/szamolo/_sz/f_LZ.html számoló]. |
== [[Soros és párhuzamos kapcsolás]] == | == [[Soros és párhuzamos kapcsolás]] == | ||
[[Kategória:Elektronikai alkatrészek]] [[Kategória: Passzív alkatrészek]] | [[Kategória:Elektronikai alkatrészek]] [[Kategória: Passzív alkatrészek]] | ||
A lap jelenlegi, 2021. május 24., 20:59-kori változata
Tartalomjegyzék
Az induktivitás áramköri szerepe
- aluláteresztő szűrő (LC vagy RL) induktivitásaként - zavarszűrés (illetve tüske elnyomás)
- kondenzátorral összekapcsolva sávszűrő (LC szűrő, rezgőkör)
- a mágneses tér összeomlasztásán alapuló feszültségcsökkentő illetve feszültségnövelő kapcsolás fojtója
Figyelem: az induktivitás nem csak mint elemi alkatrész van jelen az elektronikában, hanem bármely vezető két pontja között úgynevezett szórt induktivitás mérhető. Szerencsére az egyenes vezetőnek kicsi az induktivitása, de nagyfrekvencián nem elhanyagolható.
Az induktivitás fogalma
Az induktivitás mértékegysége a henry, jele H. Rádiótechnikában leggyakrabban a nH, µH és mH nagyságrendbe eső tekercsekkel találkozunk. Az induktivitáson (köznapi nevén tekercsen) átfolyó áram létrehoz a tekercs körül egy mágneses teret, amely mágneses tér változása ellentétesen hat az áram növekedésére. Azaz ha tekercsre egy feszültségforrást kapcsolunk, a rajta átfolyó áram nem ugrásszerűen jön létre, hanem folyamatosan növekszik. A áram növekedésének korlátozódása a tekercs induktivitása. Azaz:
<szamolo sor=5 oszlop=15 jobb>U = 4,5;L = 100 milli;t = 0,01;;I = U/L * t;</szamolo> [math]I = \frac{U}{L} \cdot t[/math]
- ahol
- I: a tekercsen átfolyó áram a feszültséggenerátor rákapcsolástól számított t idő mulva.
- U: a feszültséggenerátor feszültsége
- L: az induktivitás - amiről jelen szócikk szól.
- t: a feszültséggenerátor rákapcsolásától számított idő.
<szamolo sor=5 oszlop=34 jobb szoveg="Két egymástól D távolságra futó d átmérőjű egyenes vezető\\X méter hosszban (más szóval: 1 menetes tekercs)\\Figyelem: a hossz a párhuzamos élek hossza, nem a huzalhossz!">D = 100 milli;d = 0,8 milli;hossz = 2,5;;L = hossz * mu0/pi * ln((D-d)/d);</szamolo>
Amennyiben az árammal átjárt tekercsről hirtelen leválasztjuk a feszültségforrást, az induktivitás mágneses tere megpróbálja fenntartani a rajta átfolyó áramot, ezáltal az eredetileg pozitív tápforrás felöli kapcsán igen nagy negatív feszültség jelenik meg, amely feszültség szintén a fenti képlet szerint számítható idő alatt omlasztja össze az induktivitás mágneses terét.
- Az induktivitás a következő összefüggéssel számítható ki
- egyrészt akár a fenti mérést elvégezve, a feszültség, áramerősség és idő ismeretében.
- akár váltakozó áramon mutatott induktív reaktancia alapján, aminek speciális esete a rezgőkör rezonanciafrekvenciájából való meghatározás.
- akár a geometriai adatai és felhasznált mag fizikai paraméterei alapján az alábbi összefüggés szerint:
[math]L = \mu_0 \mu_r \frac{A}{l} N^2 = A_L \cdot N^2[/math] <szamolo sor=6 oszlop=41 jobb szoveg="Ha az egyenes tekercs hossza nagyobb, mint az átmérője.\\Például: pezsgőtablettás dobozra tekert huzal, mint légmagos tekercs.\\d = átmérő, l = mágneses erővonal hossza.">d = 28 milli;l = 2 * 50 milli;N = 57;mu_r = 1;;L=mu0*mu_r*negyzet(d/2)*pi/l*negyzet(N);</szamolo>
- ahol
- L [henry, H],
- μ0 a vákuum permeabilitása, [V*s*A-1*m-1],
- μr a relatív permeabilitás, [1],
- A a tekercs keresztmetszete, [m2] (hengeres tekercsnél (d/2)2 * pi),
- l a tekercs körül kialakuló mágneses erővonal hossza, [m] (egyenes tekercsnél 2-szerese a tekercs hosszának),
- N a tekercs menetszáma, [1],
- AL alaktényező avagy fajlagos induktivitás, elterjedt mértékegysége: nH/menet2
A vákuum permeabilitása: [math]\mu_0 = 4\pi\cdot10^{-7} \frac{V \cdot s}{A \cdot m} = 1.256\cdot10^{-6} \frac{V \cdot s}{A \cdot m} [/math], levegő esetén a relatív permeabilitás μr értéke 1.
<szamolo sor=4 oszlop=22 jobb szoveg="A<sub>L</sub> = 5400-as fazékmagra tekert 30 menet">A_L = 5400 nano;N = 30;;L = A_L * negyzet(N);</szamolo>
A induktivitás hátteréről bővebben a mágneses mező című fejezetben olvashatunk.
- Induktivitást fajlagos induktivitásból és menetszámból számoló.
- Menetszámot fajlagos induktivitásból és induktivitásból számoló.
- Fajlagos induktivitást induktivitásból és menetszámból számoló.
Az induktivitás egyenáramú körben
Az ideális tekercs kapcsaira egy ismert feszültségű forrást kapcsolva a kialakuló áram nagysága:
[math]I = \frac{U}{L} * t[/math]
- ahol
- L az induktivitás, [L] = henry = H,
- U a feszültség, [U] = volt = V,
- t a feszültség rákapcsolásának ideje, [t] = másodperc = s.
Megjegyzés: a gyakorlatban csak rövid t időre kapcsoljunk a tekercs sarkaira feszültséget, majd kapcsoljuk le róla. Ellenkező esetben a kialakuló nagy áramerősség tönkreteheti a tekercset is és a tápforrást is rövidzárral terhelheti. Egyébként a kapcsolóüzemű tápegységeknél figyelhető meg ennek a jelenségnek a gyakorlati alkalmazása.
A tekercsben tárolt energia: [math]E=\frac{1}{2} L I^2[/math].
- [E] = joule = J.
- [I] = amper = A.
A [math]\Psi = I \cdot L\,[/math] tekercsfluxust használva [math]E = \frac{1}{2} \cdot \frac{\Psi^2}{L}\,[/math].
- [Ψ] = weber = Wb.
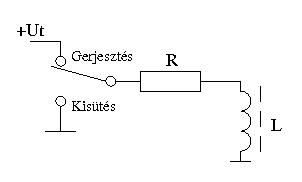
Tekintettel arra, hogy a rézhuzalból készült tekercsnek van ohmos ellenállása, nézzük meg, hogyan alakul a tekercs időbeli árama, ha rákapcsolunk egy adott feszültségű tápegységet illetve ha átkapcsoljuk a gerjesztett állapotú tekercset egy R értékű terhelőellenálláson a föld felé.
|
|
<szamolo sor=9 oszlop=39 jobb>Ut= 10;L = 47 milli;R = 100;t = 1 milli;;tau = L/R;Imax = Ut/R;Itáplált = Imax * (1 - exp(-t/tau));Iterhelt = Imax * exp(-t/tau);</szamolo>
A fenti ábra idő és feszültségtengelye relatív. Az feszültség tengely „1” értéke az ellenálláson átfolyó maximális áram értéke (Imax = Ut/R), az idő tengelyen úgynevezett τ érték szerepel, ahol τ = L/R. Például egy 47 mH értékű induktivitás 100 Ω értékű ellenálláson keresztüli táplálásakor az időtengely „1” értéke τ = L/R = 47*10-3/100 = 470 μs. A 2 pedig közel 1 ezredmásodperc és így tovább.
A τ érték azért fontos, mert 1 τ idő alatt (τ = L/R) egy induktivitás a rákapcsolt feszültség hatására a maximális áramának 63%-át folyatja már át illetve amikor egy gerjesztett állapotban levő tekercset a kisütőellenállásra kapcsolunk, akkor 37%-ára esik τ idő alatt vissza. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-át éri el gerjesztéskor az áram, illetve kisütése esetén 5 τ idő alatt már csak 0,7 % marad a tekercsben. Tehát 5 τ idő alatt egy tekercs gyakorlatilag teljesen elveszti a tárolt energiáját.
- Energiát áramerősségből és induktivitásból számoló
- Áramerősséget energiából és induktivitásból számoló
- Induktivitást energiából és áramerősségből számoló
- Induktivitást ellenállásból és időállandóból számoló
- Ellenállást induktivitásból és időállandóból számoló
- Időállandót induktivitásból és ellenállásból számoló
Az induktivitás váltakozóáramú körben
<szamolo sor=4 oszlop=17 jobb>L = 28,86 mikro;f = 7050 kilo;;X = 2*pi*f * L;</szamolo>
Az induktivitás látszólagos ellenállása adott frekvencián: [math]X_L = 2\pi \cdot f \cdot L = 6.283 \cdot f \cdot L[/math]
- ahol
- XL: a látszólagos ellenállás [Ω],
- L: az induktivitás [H] és
- f: a frekvencia [Hz].
Impedancia: [math]Z = j X_L = j 2\pi \cdot f \cdot L [ \Omega ][/math].
- Látszólagos ellenállást és impedanciát frekvenciából és induktivitásból számoló.
- Induktivitást frekvenciából és látszólagos ellenállásból vagy impedanciából számoló.
- Frekvenciát induktivitásból és látszólagos ellenállásból vagy impedanciából számoló.