„Kondenzátor” változatai közötti eltérés
(→A kondenzátor, mint elektronikai alkatrész: típusai) |
a (→Kondenzátor egyenáramú körben: + számoló linkek) |
||
| 115. sor: | 115. sor: | ||
A τ érték azért fontos, mert 1 τ idő alatt (τ = R * C) egy kondenzátor 63%-ra töltődik illetve kisütéskor 37%-ára sül ki. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-ára tölthető fel, illetve kisütése esetén 5 τ idő alatt már csak 0,7 %-a marad a kondenzátorban. Tehát 5 τ idő alatt egy kondenzátor gyakorlatilag teljesen kisül. | A τ érték azért fontos, mert 1 τ idő alatt (τ = R * C) egy kondenzátor 63%-ra töltődik illetve kisütéskor 37%-ára sül ki. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-ára tölthető fel, illetve kisütése esetén 5 τ idő alatt már csak 0,7 %-a marad a kondenzátorban. Tehát 5 τ idő alatt egy kondenzátor gyakorlatilag teljesen kisül. | ||
| + | |||
| + | * Kapacitást és energiát töltésből és feszültségből [http://hg9ieg.uw.hu/szamolo/_sz/CE_QU.html számoló] | ||
| + | * Kapacitást és töltést energiából és feszültségből [http://hg9ieg.uw.hu/szamolo/_sz/CQ_EU.html számoló] | ||
| + | * Kapacitást és feszültséget energiából és töltésből [http://hg9ieg.uw.hu/szamolo/_sz/CU_EQ.html számoló] | ||
| + | * Energiát és töltést kapacitásból és feszültségből [http://hg9ieg.uw.hu/szamolo/_sz/EQ_CU.html számoló] | ||
| + | * Energiát és feszültséget kapacitásból és töltésből [http://hg9ieg.uw.hu/szamolo/_sz/EU_CQ.html számoló] | ||
| + | * Töltést és feszültséget kapacitásból és energiából [http://hg9ieg.uw.hu/szamolo/_sz/QU_CE.html számoló] | ||
| + | * Kapacitást ellenállásból és időállandóból [http://hg9ieg.uw.hu/szamolo/_sz/CL_Rtau.html számoló] | ||
| + | * Ellenállást kapacitásból és időállandóból [http://hg9ieg.uw.hu/szamolo/_sz/LR_Ctau.html számoló] | ||
| + | * Időállandót kapacitásból és ellenállásból [http://hg9ieg.uw.hu/szamolo/_sz/Ltau_CR.html számoló] | ||
== Kondenzátor váltakozó áramú körben == | == Kondenzátor váltakozó áramú körben == | ||
A lap 2011. június 28., 13:57-kori változata
Tartalomjegyzék
- 1 A kondenzátor feladata
- 2 A kapacitás alapfogalma
- 3 Kondenzátor egyenáramú körben
- 4 Kondenzátor váltakozó áramú körben
- 5 A kondenzátor, mint elektronikai alkatrész
- 5.1 A kondenzátor kapacitása
- 5.2 A kondenzátor terhelhetősége
- 5.3 A kondenzátorok járulékos paraméterei
- 5.4 Néhány kondenzátor típus
- 5.4.1 Fix, légszigetelésű
- 5.4.2 Fix, kerámia
- 5.4.3 Fix, papír
- 5.4.4 Fix, műanyag szigetelésű
- 5.4.5 Fix, elektrolit
- 5.4.6 Fix, tantál
- 5.4.7 Fix, beállító
- 5.4.8 Beállító, légszigetelésű
- 5.4.9 Beállító, kerámia
- 5.4.10 Beállító, műanyag szigetelésű
- 5.4.11 Változtatható, vákuum szigetelésű
- 5.4.12 Változtatható, levegő szigetelésű
- 5.4.13 Változtatható, műanyag szigetelésű
- 5.4.14 Varikap
A kondenzátor feladata
- energiatárolás (rövidtávú)
- zajsimítás (váltakozóáramú komponensek csillapítása = hidegítés)
- egyenáramú komponens leválasztása
- induktivitással összekapcsolva rádiófrekvenciás frekvenciaszűrőt készíthetünk
- ellenállással összekapcsolva hangfrekvenciás szűrő készíthető
Lásd még: zavarszűrő kondenzátorok
A kapacitás alapfogalma
A kapacitás oly módon képzelhető el, mint egy víztartály, amelyben
- a vízszint megfeleltethető a feszültségnek,
- a beáramló illetve kiáramló vízmennyiség az áramerősségnek.
Így a kapacitásról elmondható, hogy a bele folyó áram tölti fel valamekkora feszültségre. Hogy mekkorára?
[math]U = \frac{Q}{C} = \frac{I}{C} \cdot t[/math]
| Anyag | Relatív permittivitás |
|---|---|
| Vákuum: | 1 |
| Levegő | 1,00059 |
| Fém | 1 |
| Üveg | 5 .. 7 |
| Kerámia | 9,5 .. 100 |
| Desztillált víz | 81 |
| Báriumtitanát | 103 .. 104 |
| NYÁK lap | körülbelül 2,5 |
- ahol
- U: a feszültség, amelyre feltöltődött
- Q: a beáramló töltés mennyisége
- I: az áramerősség, amely tölti
- C: a kapacitás nagysága - amiről ez a szócikk szól.
- t: az üres kondenzátorra rákapcsolt I áram általi töltés ideje.
- A kapacitás kiszámítása
- egyrészt akár a fenti mérést elvégezve, a feszültség, áramerősség és idő ismeretében.
- akár váltakozó áramon mutatott induktív reaktancia alapján, aminek speciális esete a rezgőkör rezonanciafrekvenciájából való meghatározás.
- akár a geometriai adatai és felhasznált dielektrikum (szigetelő) fizikai paraméterei alapján az alábbi összefüggés szerint:
[math]C = \varepsilon_0 \varepsilon_r \frac{A}{d}[/math]
- ahol
<szamolo sor=7 oszlop=15 jobb>a = 30 milli;b = 20 milli;d = 1 milli;er = 2;;A = a*b;C = e0*er*A/d;</szamolo>
- C a kapacitás [farad, F],
- ε a permittivitás
- ε0 a vákum permittivitása [A*s*V-1*m-1],
- εr pedig az adott anyag vákuumhoz képesti szorzója [1]
- A az egymással szemben álló fegyverzetek területe [m2]
- d a fegyverzetek közti távolság [m]
Vákum permittivitása: [math]\varepsilon_0 = 8.85*10^{-12} \frac{A s}{V m}[/math]
A témáról bővebben az elektromos mező című fejezetben.
Kapacitás mértékegysége
SI-egysége a farad, jele F. 1 F = 1 C/V = 1 m-2*kg-1*s4*A2.
Cgs-ben ( ~1950. előtti kapcsolásokban ) 1 cm = c-2*105 F ~ 1.112650056053618432174089964848 pF.
( c = 299792458 m/s, fénysebesség ).
Kondenzátor egyenáramú körben
A kondenzátor által tárolt töltés: Q = C * U = I * t, azaz a kapacitás szorozva a kondenzátor feszültségével. Ugyanakkor úgy is felírhatjuk, hogy állandó töltő áramerősséget feltételezve a töltő áramerősség és az idő szorzata. Ebből az az is látható, hogy állandó áramerősséggel töltve egy kondenzátort, U = Q/C = I/C * t. Azaz az idő függvényében egyenletesen tesz szert nagyobb feszültségre, ahol a töltődés meredeksége az áramerősség és a kapacitás hányadosa. Természetesen ez megfordítva a kisütés folyamatára is érvényes.
Egy másik fontos tényező a kondenzátor által tárolt energia: [math]E=\frac{1}{2}CU^2[/math].
A gyakorlatban legtöbbször nem állandó árammal töltődik a kondenzátor, hanem egy soros ellenálláson keresztül. A kondenzátor egy vele sorba kapcsolt ellenálláson történő feltöltése illetve egy párhuzamosan kapcsolt ellenálláson keresztüli kisütése exponenciális függvénnyel írható le. Ennek okát egyszerűen megérthetjük, ha arra gondolunk, hogy az üres kondenzátor feltöltésének kezdetekor az ellenállásra Ut feszültség jut, amely árama I=U/R összefüggéssel kiszámítható, de például egy már félig feltöltött kondenzátor esetén a töltőáram már csak a fele értékű, azaz a töltési sebesség ezen pontban már csak a fele.
<szamolo sor=8 oszlop=30 jobb>Ut = 10;R = 1 kilo;C = 100 mikro;t = 0,150;;tau = R * C;Utölt = Ut * (1-exp(-t/tau));Ukisüt= Ut * exp(-t/tau);</szamolo>
Feltöltés: [math]U_C = U_t * ( 1 - e^{-\frac{t}{\tau}} ) = U_t * ( 1 - e^{-\frac{t}{R * C}} )[/math]
Kisütés: [math]U_C = U_t * e^{-\frac{t}{\tau}} = U_t * e^{-\frac{t}{R * C}}[/math], ahol
- UC a kondenzátor feszültsége [V]
- Ut a tápfeszültség [V]
- t az eltelt idő [s]
- τ a kapcsolás időállandója [s]
- R az ellenállás értéke [Ω]
- C a kondenzátor kapacitása [F]
|
|
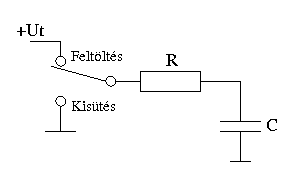
A fenti ábra idő és feszültségtengelye relatív. Az feszültség tengely „1” értéke az ellenálláson keresztül rákapcsolt feszültség értéke, az idő tengelyen úgynevezett τ érték szerepel, ahol τ = R * C. Például egy 10 0μF értékű kondenzátor 47 kΩ értékű ellenálláson keresztüli töltésekor az időtengely „1” értéke τ = R * C = 100*10-6 * 47*103 = 4,7 másodperc. A 2 pedig a 9,4 másodperc és így tovább.
A τ érték azért fontos, mert 1 τ idő alatt (τ = R * C) egy kondenzátor 63%-ra töltődik illetve kisütéskor 37%-ára sül ki. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-ára tölthető fel, illetve kisütése esetén 5 τ idő alatt már csak 0,7 %-a marad a kondenzátorban. Tehát 5 τ idő alatt egy kondenzátor gyakorlatilag teljesen kisül.
- Kapacitást és energiát töltésből és feszültségből számoló
- Kapacitást és töltést energiából és feszültségből számoló
- Kapacitást és feszültséget energiából és töltésből számoló
- Energiát és töltést kapacitásból és feszültségből számoló
- Energiát és feszültséget kapacitásból és töltésből számoló
- Töltést és feszültséget kapacitásból és energiából számoló
- Kapacitást ellenállásból és időállandóból számoló
- Ellenállást kapacitásból és időállandóból számoló
- Időállandót kapacitásból és ellenállásból számoló
Kondenzátor váltakozó áramú körben
A kondenzátorra ( szinuszos ) váltakozóáramú jelet kapcsolva látszólagos ellenállást mutat. Értéke:
[math]X_C=\frac{1}{2\pi f C}[/math]
- ahol
- Xc képzetes ellenállás [Ω],
- f a frekvencia [Hz],
- C a kapacitás [F].
Példa: egy 10 nF-os kondenzátor 455 kHz-en mekkora képzetes ellenállást mutat?
<szamolo sor=4 oszlop=20>C = 10 nano;f = 455 kilo;;Xc = 1/(2*pi*f * C)</szamolo>
Tehát 34,979 ohm kapacitív reaktanciát (képzetes ellenállást) mutat ezen a frekvencián.
- Impedancia
- [math]Z = -j X_C = -j \frac{1}{2\pi f C}[/math]
Az előző példa adataival Z = -j 34.98 Ω
Megjegyzés: [math]\frac{1}{j} = -j[/math].
Lásd még:
- Látszólagos ellenállást és impedanciát kapacitásból és frekvenciából számoló.
- Kapacitást frekvenciából és látszólagos ellenállásból vagy impedanciából számoló.
- Frekvenciát kapacitásból és látszólagos ellenállásból vagy impedanciából számoló.
A kondenzátor, mint elektronikai alkatrész
A kondenzátor kapacitása
A kondenzátorokat E12-es sor szerint célszerű az áramkörbe tervezni, azaz 1 - 1,2 - 1,5 - 1,8 - 2,2 - 2,7 - 3,3 - 3,9 - 4,7 - 5,6 - 6,8 - 8,2. Ezek ±10 %. Van néhány gyártó ±20 % pontos értékeket garantál.
A nagy, 1 mikrofarád (μF) vagy annál nagyobb kondenzátorok esetén az E6-os sor szerinti 1 - (1,5 ritkán) - 2,2 - 3,3 - 4,7 - 6,8 értéksor szerint érdemes választani. Ezek ±20 % pontosságúak.
- Furatszerelt
- Kerámiakondenzátor: 2,2 pF .. 2,2 μF között
- Fóliakondenzátor: 0,1 nF .. 100 μF között
- Tantál elektrolit kondenzátor: 0,1 μF .. 1000 μF között
- Alu elektrolit kondenzátor: 0,47 μF .. 100.000 μF között
- Szuperkapacitások: 200 farad kapacitásig (2010. évben)
- Felületszerelt
- Kerámiakondenzátor: 0,47 pF .. 100 μF között
- Fóliakondenzátor: 1 nF .. 10 μF között
- Tantál elektrolit kondenzátor: 0,1 μF .. 1000 μF között
- Alumínium elektrolit kondenzátor: 1 μF .. 1000 μF között
A kondenzátor terhelhetősége
A kondenzátor esetén a maximálisan rákapcsolható feszültséget adják meg, amit átütés nélkül elvisel. Elektrolit kondenzátor és a szuperkapacitások esetén ügyeljünk a helyes polaritásra. Ezek ugyanis csak egyféle, rajtuk feltüntetett polaritást viselnek el károsodás nélkül.
Elektrolit kondenzátorok nagy kapacitással rendelkeznek, ellenben nagyfrekvenciás tulajdonságaik igen rosszak. Ezt a velük párhuzamosan kötött kerámiakondenzátorral szoktuk kiküszöbölni. Az elektrolit kondenzátor további rossz tulajdonsága, hogy 10 év alatt jelentős mértékben kiszárad, veszít kapacitásából és a soros ellenállása (lásd alább) is rosszabb lesz. Ez a kiszáradási folyamat az aktív igénybevétel, például a kapcsolóüzemű tápegység pufferkondenzátoraként alkalmazva felgyorsul.
A kondenzátorok járulékos paraméterei
A képen látható modellel modellezhető a valódi alkatrész, ahol:
- Rpar: párhuzamos ellenállása a tokozásnak. MΩ nagyságrendű, így a gyakorlatban elhanyagolható.
- Cpar: elektródák közötti pF-os nagyságrendű kapacitás. Ez egyúttal a valódi áramkör alkatrészei közötti szórt kapacitás problémáira is ráirányítja a figyelmünket.
- Rser vagy más néven ESR (Equivalent Series Resistance = megfeleltetett soros ellenállás): főként elektrolit kondenzátoroknál jelentős. Az ESR-be beleszámít az elektrolitban levő ionok vándorlásának lomhasága is, amely villamos szempontból tényleg ellenállásként jelentkezik. Kapcsolóüzemű tápegységekben jelentős lüktető feszültséget jelent, ha rossz ESR-rel rendelkező elektrolit kondenzátorral simítjuk a kimenőfeszültséget.
- Capacitance: végre itt van az, amiért kondenzátort tettünk az áramkörbe. A kapacitása.
- Lser: egyetlen betáplálással rendelkező tekercselt kondenzátoroknál (fólia vagy feltekercselt elektrolit) esetén 10..100 mH is lehet. Ez az oka a rossz nagyfrekvenciás viselkedésnek. Kerámiakondenzátorok esetén kicsi.
- RLshunt: a modell szerint a tekercselt rész közötti szivárgás. Hatása elhanyagolható.
A fentiek közül a vastagon kiemelt ESR és a soros induktivitás az a kettő paraméter, amelyre speciális áramkörök tervezésekor oda kell figyelni.
Néhány kondenzátor típus
Fix, légszigetelésű
Fix, kerámia
Fix, papír
Fix, műanyag szigetelésű
Fix, elektrolit
Fix, tantál
Fix, beállító
Néhány pF-os kondenzátort úgy is készíthetsz, ha két vezetéket összetekersz, vagy a vastagabbra vékonyat rátekersz. Legalább az egyik vezeték szigetelt, mechanikai stabilitás miatt tömörek legyenek. Az így készült kondenzátor kukactrimmer vagy hernyótrimmer.