„Rezgőkör” változatai közötti eltérés
(Új oldal, tartalma: „==Soros RLC kör== Az ohmos és reaktáns elemekből összeállított áramkörök között kitüntetett szerepe van a kondenzátorból, tekercsből (és ellenállásbó...”) |
a (Link: Thomson-képlet) |
||
| (3 közbenső módosítás, amit egy másik szerkesztő végzett, nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | + | =Soros RLC kör= | |
| − | Az ohmos és reaktáns elemekből összeállított áramkörök között kitüntetett szerepe van a | + | Az ohmos és reaktáns elemekből összeállított áramkörök között kitüntetett szerepe van a [[kondenzátor]]ból ('''C'''), [[induktivitás]]ból (tekercsből, '''L''') és [[ellenállás]]ból ('''R''') álló áramkörnek. |
| − | + | Az ellenállást gyakorlati számításokban nem célszerű kihagyni - még ha magában az áramkörben nincs is ellenállás-, így vehetjük ugyanis figyelembe a valóságos tekercs veszteségi ellenállását. | |
| − | |||
| + | A fenti elemekból álló soros áramkört és a fázisviszonyokat az 1. ábrán láthatjuk. A soros RLC kört később tisztázandó okból ''soros rezgőkörnek'' nevezik. | ||
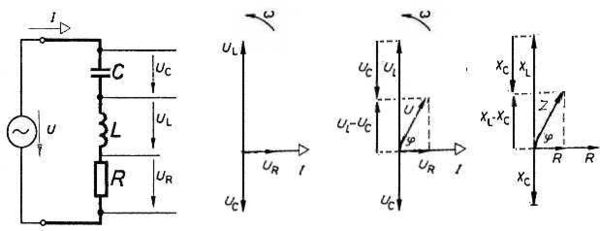
| − | [[Kép:R1.jpg|center | + | [[Kép:R1.jpg|center|thumb|600px|1. ábra]] |
| − | |||
| − | Mindhárom sorba kapcsolt elemen ugyanaz az I áram folyik keresztül, a vektorábrán ezt a vízszintesen jobbra mutató I vektor jelzi. Az ellenálláson eső | + | Mindhárom sorba kapcsolt elemen ugyanaz az I áram folyik keresztül, a vektorábrán ezt a vízszintesen jobbra mutató I vektor jelzi. Az ellenálláson eső <math>U_R</math> feszültség fázisban van az árammal, ezért azzal azonos irányú. A tekercsen indukálódó <math>U_L</math> feszültség az áramhoz képest 90 fokkal siet, ezért függőleges, felfelé irányított vektor jelzi. A kondenzátoron eső UC feszültség az átfolyó áramhoz képest 90 fokkal késik, ezért az ennek megfelelő vektor lefelé irányul (bal oldali vektorábra). |
| − | A generátor U feszültsége e három feszültség ( | + | A generátor U feszültsége e három feszültség (<math>U_R, U_L, U_C</math>) vektori eredője. Mivel <math>U_L</math> és <math>U_C</math> ellentétes irányú, e két feszültség eredője a két feszültség különbsége; a példában <math>U_L</math> a nagyobb értékű, ezért a különbségi feszültség (<math>U_L-U_C</math>) vektora felfelé irányul. Ezt a feszültséget kell vektori módon összegezni <math>U_R</math>–el (középső vektorábra), az eredő U feszültséggel egyezik meg. |
| − | Az impedancia kiszámításához (jobb oldali vektorábra) valamennyi feszültséget elosztottuk I árammal, így olyan derékszögű háromszög adódik, melynek átfogója Z, befogói R és ( | + | Az [[impedancia]] kiszámításához (jobb oldali vektorábra) valamennyi feszültséget elosztottuk I árammal, így olyan derékszögű háromszög adódik, melynek átfogója Z, befogói R és (<math>X_L-X_C</math>). |
| − | Tekintettel arra, hogy | + | Tekintettel arra, hogy <math>X_L</math> és <math>X_C</math> a frekvencia függvényében változik, Z értéke is a frekvenciától függ (2. ábra). Azon a frekvencián, ahol <math>X_L = X_C</math>, a két mennyiség különbsége 0, és itt Z = R, azaz az áramkör R-el megegyező ohmos ellenállást tanúsít. Ezt a frekvenciát ''rezonanciafrekvenciának'' nevezik és f<sub>0</sub>- al (az ennek megfelelő körfrekvenciát ω<sub>o</sub>-al) jelölik. |
| − | Mivel | + | Mivel <math>X_L</math> = ωL, és <math>X_C</math> = 1/ωC, és a rezonanciafrekvencián e két mennyiség egyenlő, ahonnan |
ω<sub>o</sub><sup>2</sup> =1/LC | ω<sub>o</sub><sup>2</sup> =1/LC | ||
adódik. | adódik. | ||
| − | |||
| − | Ez, a rezonanciafrekvencia meghatározására szolgáló képlet az ún. Thomson-képlet. | + | Ez, a rezonanciafrekvencia meghatározására szolgáló képlet az ún. [[Thomson-képlet]]. |
| − | + | [[Kép:R2.jpg|center|thumb|600px|2. ábra]] | |
| − | |||
| − | [[Kép:R2.jpg|center | ||
| − | |||
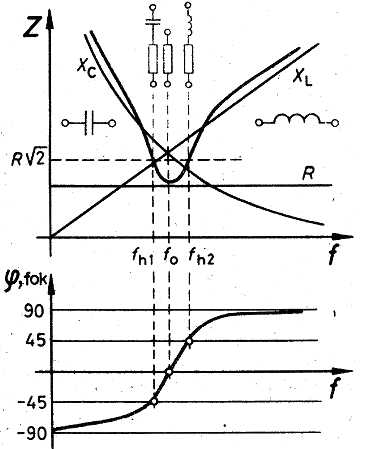
A 2. ábrán Z impedanciát (és annak komponenseit) ill. a fázisszöget ábrázoltuk a frekvencia függvényében. | A 2. ábrán Z impedanciát (és annak komponenseit) ill. a fázisszöget ábrázoltuk a frekvencia függvényében. | ||
| 39. sor: | 34. sor: | ||
Z komponensei: | Z komponensei: | ||
| − | + | * R, melynek ellenállása a frekvencia függvényében nem változik, | |
| − | + | * <math>X_L</math> = ωL a frekvenciával arányosan nő, | |
| − | + | * <math>X_C</math> = 1/ωC a frekvencia növekedtével a görbe szerint csökken. | |
| − | Kis frekvenciákon (f << f0) a három komponens közül | + | Kis frekvenciákon (f << f0) a három komponens közül <math>X_C</math> a domináns, a soros RLC kör mint sorosan kapcsolt ellenállás és kondenzátor viselkedik, ennek megfelelően a fázisszög is a kapacitív reaktancia –90 fokos szögéhez közelít. |
Rezonanciafrekvencián (f = f0) a kapacitív és induktív reaktancia megegyezik, de ellentétes fázisszögüknél fogva „kiejtik egymást”, és a rezgőkör csak R ellenállást mutatja. | Rezonanciafrekvencián (f = f0) a kapacitív és induktív reaktancia megegyezik, de ellentétes fázisszögüknél fogva „kiejtik egymást”, és a rezgőkör csak R ellenállást mutatja. | ||
A frekvencia növekedtével (f >> f0) egyre inkább az induktív reaktancia válik dominánssá, a soros RLC kör mint ellenállás és sorba kapcsolt tekercs viselkedik, e szerint alakul a +90 fokhoz közelítő fázisszög is (ilyen a viszonyokat mutatnak be az 1. ábra vektordiagramjai is). | A frekvencia növekedtével (f >> f0) egyre inkább az induktív reaktancia válik dominánssá, a soros RLC kör mint ellenállás és sorba kapcsolt tekercs viselkedik, e szerint alakul a +90 fokhoz közelítő fázisszög is (ilyen a viszonyokat mutatnak be az 1. ábra vektordiagramjai is). | ||
| − | Nagy jelentősége van annak a két frekvenciának, amelynél a rezgőkör impedanciájának valós és képzetes része megegyezik ( | + | Nagy jelentősége van annak a két frekvenciának, amelynél a rezgőkör impedanciájának valós és képzetes része megegyezik (<math>f_{h1}, f_{h2}</math>). Ezeken a frekvenciákon <math>R=X_L-X_C</math> vagy <math>R=X_C-X_L</math>, így <math>Z=\sqrt{2} R</math>. |
| − | Az | + | Az <math>f_{h2}-f_{h1}</math> frekvenciakülönbséget a rezgőkör ''sávszélességének'' nevezik, és B–vel jelölik (mértékegysége: Hz): |
| − | B = | + | B = <math>f_{h2}-f_{h1}</math> |
| − | A rezonanciafrekvencia és a sávszélesség hányadosa a rezgőkör jósága, jele: Q (mértékegység nélküli viszonyszám) | + | A rezonanciafrekvencia és a sávszélesség hányadosa a rezgőkör ''jósága'', jele: Q (mértékegység nélküli viszonyszám): |
| + | Q = f0/B. | ||
| − | + | =Párhuzamos rezgőkör= | |
R ellenállás, C kondenzátor és L tekercs párhuzamos kapcsolásával párhuzamos rezgőkörhöz jutunk (3. ábra). | R ellenállás, C kondenzátor és L tekercs párhuzamos kapcsolásával párhuzamos rezgőkörhöz jutunk (3. ábra). | ||
| 65. sor: | 61. sor: | ||
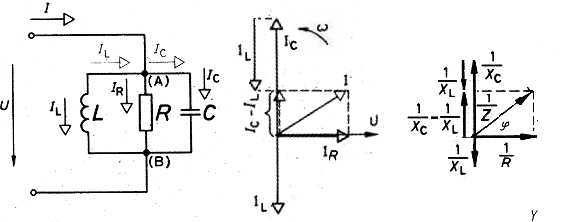
| − | [[Kép:R3.jpg|center | + | [[Kép:R3.jpg|center|thumb|600px|3. ábra]] |
| − | |||
A lap jelenlegi, 2010. július 24., 10:52-kori változata
Soros RLC kör
Az ohmos és reaktáns elemekből összeállított áramkörök között kitüntetett szerepe van a kondenzátorból (C), induktivitásból (tekercsből, L) és ellenállásból (R) álló áramkörnek. Az ellenállást gyakorlati számításokban nem célszerű kihagyni - még ha magában az áramkörben nincs is ellenállás-, így vehetjük ugyanis figyelembe a valóságos tekercs veszteségi ellenállását.
A fenti elemekból álló soros áramkört és a fázisviszonyokat az 1. ábrán láthatjuk. A soros RLC kört később tisztázandó okból soros rezgőkörnek nevezik.
Mindhárom sorba kapcsolt elemen ugyanaz az I áram folyik keresztül, a vektorábrán ezt a vízszintesen jobbra mutató I vektor jelzi. Az ellenálláson eső [math]U_R[/math] feszültség fázisban van az árammal, ezért azzal azonos irányú. A tekercsen indukálódó [math]U_L[/math] feszültség az áramhoz képest 90 fokkal siet, ezért függőleges, felfelé irányított vektor jelzi. A kondenzátoron eső UC feszültség az átfolyó áramhoz képest 90 fokkal késik, ezért az ennek megfelelő vektor lefelé irányul (bal oldali vektorábra).
A generátor U feszültsége e három feszültség ([math]U_R, U_L, U_C[/math]) vektori eredője. Mivel [math]U_L[/math] és [math]U_C[/math] ellentétes irányú, e két feszültség eredője a két feszültség különbsége; a példában [math]U_L[/math] a nagyobb értékű, ezért a különbségi feszültség ([math]U_L-U_C[/math]) vektora felfelé irányul. Ezt a feszültséget kell vektori módon összegezni [math]U_R[/math]–el (középső vektorábra), az eredő U feszültséggel egyezik meg.
Az impedancia kiszámításához (jobb oldali vektorábra) valamennyi feszültséget elosztottuk I árammal, így olyan derékszögű háromszög adódik, melynek átfogója Z, befogói R és ([math]X_L-X_C[/math]).
Tekintettel arra, hogy [math]X_L[/math] és [math]X_C[/math] a frekvencia függvényében változik, Z értéke is a frekvenciától függ (2. ábra). Azon a frekvencián, ahol [math]X_L = X_C[/math], a két mennyiség különbsége 0, és itt Z = R, azaz az áramkör R-el megegyező ohmos ellenállást tanúsít. Ezt a frekvenciát rezonanciafrekvenciának nevezik és f0- al (az ennek megfelelő körfrekvenciát ωo-al) jelölik.
Mivel [math]X_L[/math] = ωL, és [math]X_C[/math] = 1/ωC, és a rezonanciafrekvencián e két mennyiség egyenlő, ahonnan
ωo2 =1/LC
adódik.
Ez, a rezonanciafrekvencia meghatározására szolgáló képlet az ún. Thomson-képlet.
A 2. ábrán Z impedanciát (és annak komponenseit) ill. a fázisszöget ábrázoltuk a frekvencia függvényében.
Z komponensei:
- R, melynek ellenállása a frekvencia függvényében nem változik,
- [math]X_L[/math] = ωL a frekvenciával arányosan nő,
- [math]X_C[/math] = 1/ωC a frekvencia növekedtével a görbe szerint csökken.
Kis frekvenciákon (f << f0) a három komponens közül [math]X_C[/math] a domináns, a soros RLC kör mint sorosan kapcsolt ellenállás és kondenzátor viselkedik, ennek megfelelően a fázisszög is a kapacitív reaktancia –90 fokos szögéhez közelít. Rezonanciafrekvencián (f = f0) a kapacitív és induktív reaktancia megegyezik, de ellentétes fázisszögüknél fogva „kiejtik egymást”, és a rezgőkör csak R ellenállást mutatja. A frekvencia növekedtével (f >> f0) egyre inkább az induktív reaktancia válik dominánssá, a soros RLC kör mint ellenállás és sorba kapcsolt tekercs viselkedik, e szerint alakul a +90 fokhoz közelítő fázisszög is (ilyen a viszonyokat mutatnak be az 1. ábra vektordiagramjai is).
Nagy jelentősége van annak a két frekvenciának, amelynél a rezgőkör impedanciájának valós és képzetes része megegyezik ([math]f_{h1}, f_{h2}[/math]). Ezeken a frekvenciákon [math]R=X_L-X_C[/math] vagy [math]R=X_C-X_L[/math], így [math]Z=\sqrt{2} R[/math].
Az [math]f_{h2}-f_{h1}[/math] frekvenciakülönbséget a rezgőkör sávszélességének nevezik, és B–vel jelölik (mértékegysége: Hz):
B = [math]f_{h2}-f_{h1}[/math]
A rezonanciafrekvencia és a sávszélesség hányadosa a rezgőkör jósága, jele: Q (mértékegység nélküli viszonyszám):
Q = f0/B.
Párhuzamos rezgőkör
R ellenállás, C kondenzátor és L tekercs párhuzamos kapcsolásával párhuzamos rezgőkörhöz jutunk (3. ábra).
A párhuzamos áramköri elemek mindegyikére U szinuszos váltakozó feszültség kapcsolódik (a bal oldali vektorábrán a feszültség vektora vízszintesen, jobbra irányul). Az ellenálláson átfolyó IR áram a feszültséggel fázisban van, vektora ugyanebbe az irányba mutat. A kondenzátoron IC áram a feszültséghez képest 90 fokkal siet, vektora függőlegesen felfelé irányul. A tekercs IL árama 90 fokkal késik, vektora függőlegesen lefelé mutat.
A rezgőkörön kialakuló I áram IR, IL és IC vektori összegeként adódik. IL és IC ellenfázisú, egymásból kivonódnak. Az ábrán IC a nagyobb, ezért eredőjük IC irányú, nagysága IC – IL (középső ábrarész). Ha most mindegyik áramot elosztjuk a közös U feszültséggel, az ellenállás ill. a reaktanciák reciprokát kapjuk (az ábra jobb oldalán). 1/Z egy derékszögű háromszög átfogója, 1/R és (1/XC-1/XL) a befogói.
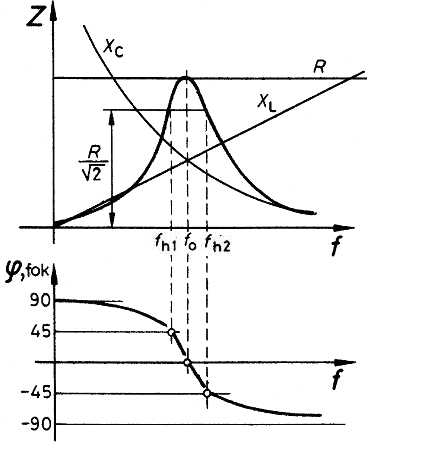
Ugyanúgy mint a soros rezgőkörnél, azt az f0 frekvenciát, ahol XC = XL rezonanciafrekvenciának nevezik. (Meghatározása a Thomson-képlet segítségével történik). Ezen a frekvencián a kondenzátoron és a tekercsen ellentétes irányú, azonos nagyságú áram folyik, ezek egymást kiegyenlítik, és a rezgőkör R ohmos ellenállást tanúsít. Minden más frekvencián reaktáns áram is folyik, ezért a rezgőkör impedanciája csökken (4. ábra).
Kisebb frekvenciákon a tekercs jelenti a kisebb reaktanciát, így a rezgőkör impedanciája induktív jellegű, míg a rezonanciafrekvencia felett a kapacitív reaktancia a kisebb, ezért az impedancia kapacitív jellegű.
- 4.ábra
A sávszélesség annak a két frekvenciának (fh2 és fh1) a különbsége, ahol a párhuzamos rezgőkör impedanciája a rezonanciafrekvencián mért érték gyök 2-ed részére csökken:
B = fh2 - fh1
Hogyan „rezeg” a rezgőkör?
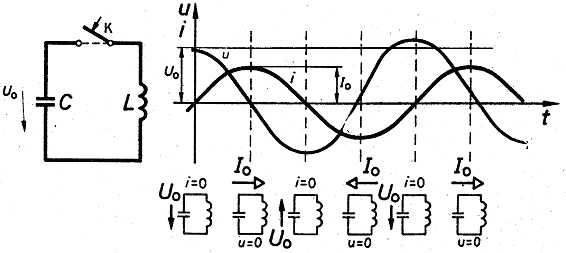
Töltsük fel az 5. ábrán látható C kondenzátort U0 feszültségre, majd zárjuk a K kapcsolót.
- 5. ábra
Az összekapcsolás pillanatától mindkét elemen ugyanakkora áram folyik, és ugyanakkora a feszültség is.
A t = 0 időpontban a kondenzátor U0 feszültségre van feltöltve, áram nem folyik. A feszültség hatására a tekercsen egyre nagyobb áram indul meg, amely a kondenzátort fokozatosan kisüti. Amikor a kondenzátor teljesen kisült, a feszültség 0, ugyanekkor folyik a legnagyobb áram (a feltöltött kondenzátorban tárolt energia ekkor teljes egészében mágneses energiává alakul). Ennek az energiának a hatására a tekercsen az áram tovább folyik, és – az előzővel ellentétes polaritással – tölteni kezdi a kondenzátort. Amikor a kondenzátor –U0 feszültségre töltődött, az áram ismét 0-ra csökken: a mágneses energia teljes egészében elektrosztatikus energiává alakult vissza. A folyamat ciklikusan ismétlődik, a feszültség és az áram lefolyását az ábra jobb oldalán láthatjuk. (Mindkét elemen az ismert 90 fokos fáziseltérés van a feszültség és az áram között.)
Tehát a „magára hagyott” LC körben szinuszos rezgés alakult ki, az ilyen elrendezést ezért nevezik rezgőkörnek.
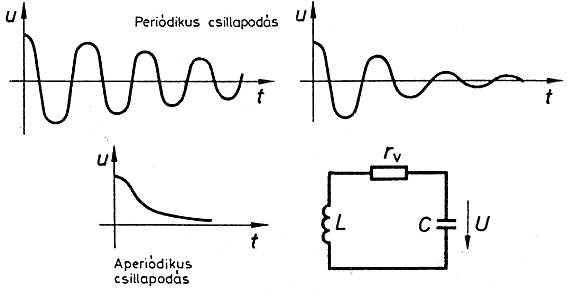
Ha a rezgőkör ideális (veszteség nélküli) kondenzátorból és tekercsből áll, a rezgés az idők végeztéig fennmarad. A valóságban a rezgőkör elemei veszteségesek, ezt gyakorlati számításokkor a rezgőkörbe helyezett ellenállással vesszük figyelembe. A veszteségek miatt a rezgés amplitúdója folyamatosan csökken (6. ábra).
- 6. ábra
Minél nagyobb a rezgőkör jósága (Q-ja), annál hosszabb idő alatt csillapodnak a rezgőkör rezgései. Csekély jóságú rezgőkörnél egy teljes rezgési periódus sem zajlik le (aperiodikus csillapítás).