Induktivitás

Az induktivitás feladata

• aluláteresztő szűrő (LC vagy RL) induktivitásaként - zavarszűrés (illetve tüske elnyomás)
• kondenzátorral összekapcsolva sávszűrő (LC szűrő, rezgőkör)
• a mágneses tér összeomlasztásán alapuló feszültségcsökkentő illetve feszültségnövelő kapcsolás fojtója

Az induktivitás fogalma

Az induktivitás mértékegysége a Henry, jele H. Rádiótechnikában leggyakrabban a nH, µH és mH nagyságrendbe eső tekercsekkel találkozunk. Az induktivitáson (köznapi nevén tekercsen) átfolyó áram létrehoz a tekercs körül egy mágneses teret, amely mágneses tér változása ellentétesen hat az áram növekedésére. Azaz ha tekercsre egy feszültségforrást kapcsolunk, a rajta átfolyó áram nem ugrásszerűen jön létre, hanem folyamatosan növekszik. A áram növekedésének korlátozódása a tekercs induktivitása. Azaz:

<szamolo jobb>U = 4,5;L = 100 milli;t = 0,01;;I = U/L * t;</szamolo> [math]I = \frac{U}{L} \cdot t[/math]

ahol

• I: a tekercsen átfolyó áram a feszültséggenerátor rákapcsolástól számított t idő mulva.
• U: a feszültséggenerátor feszültsége
• L: az induktivitás - amiről jelen szócikk szól.
• t: a feszültséggenerátor rákapcsolásától számított idő.

Amennyiben az árammal átjárt tekercsről hirtelen leválasztjuk a feszültségforrást, az induktivitás mágneses tere megpróbálja fenntartani a rajta átfolyó áramot, ezáltal az eredetileg pozitív tápforrás felöli kapcsán igen nagy negatív feszültség jelenik meg, amely feszültség szintén a fenti képlet szerint számítható idő alatt omlasztja össze az induktivitás mágneses terét.

Az induktivitás a következő összefüggéssel számítható ki

• egyrészt akár a fenti mérést elvégezve, a feszültség, áramerősség és idő ismeretében.
• akár váltakozó áramon mutatott induktív reaktancia alapján, aminek speciális esete a rezgőkör rezonanciafrekvenciájából való meghatározás.
• akár a geometriai adatai és felhasznált mag fizikai paraméterei alapján az alábbi összefüggés szerint:

<szamolo sor=6 oszlop=40>d = 30 milli;l = 2 * 50 milli;N = 57;mu_r = 1;;L=mu0*mu_r*negyzet(d/2)*pi/l*negyzet(N);</szamolo>

Pezsgőtablettás dobozra tekert huzal, mint légmagos tekercs példa. d = átmérő, l = mágneses erővonal hossza.

[math]L = \mu_0 \mu_r \frac{A}{l} N^2 = A_L \cdot N^2[/math]

ahol

• L [henry, H],
• μ₀ a vákuum permeabilitása, [V*s*A^-1*m^-1],
• μ_r a relatív permeabilitás, [1],
• A a tekercs keresztmetszete, [m²] (hengeres tekercsnél (d/2)² * pi),
• l a tekercs körül kialakuló mágneses erővonal hossza, [m] (egyenes tekercsnél 2-szerese a tekercs hosszának),
• N a tekercs menetszáma, [1],
• A_L alaktényező avagy fajlagos induktivitás, elterjedt mértékegysége: nH/menet²

A vákuum permeabilitása: [math]\mu_0 = 4\pi\cdot10^{-7} \frac{V \cdot s}{A \cdot m} = 1.256\cdot10^{-6} \frac{V \cdot s}{A \cdot m} [/math], levegő esetén a relatív permeabilitás μ_r értéke 1.

A induktivitás hátteréről bővebben a mágneses mező című fejezetben olvashatunk.

Az induktivitás talán egy fizikai jelenség, ami csökkenti a vezetőben kialakuló áramot a frekvencia függvényében. A főleg a vezető hosszától függ. Ezért gyakran feltekercselik, hogy közelebb legyen a másik vége. Az ilyen feltekercselt vezetéket nevezik tekercsnek. Van kezdete és vége. Mint egy logikus gondolatsornak. Amit érdemes előterjeszteni.

• Induktivitást   fajlagos induktivitásból és menetszámból számoló.
• Menetszámot   fajlagos induktivitásból és induktivitásból számoló.
• Fajlagos induktivitást   induktivitásból és menetszámból számoló.

Az induktivitás egyenáramú körben

A tekercsben tárolt energia: [math]E=\frac{1}{2} L I^2[/math].

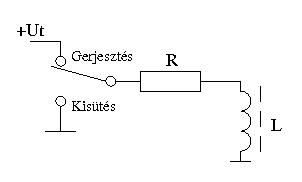
Tekintettel arra, hogy a rézhuzalból készült tekercsnek van ohmos ellenállása, nézzük meg, hogyan alakul a tekercs időbeli árama, ha rákapcsolunk egy adott feszültségű tápegységet illetve ha átkapcsoljuk a gerjesztett állapotú tekercset egy R értékű terhelőellenálláson a föld felé.

A fenti ábra idő és feszültségtengelye relatív. Az feszültség tengely „1” értéke az ellenálláson átfolyó maximális áram értéke (I_max = U_t/R), az idő tengelyen úgynevezett τ érték szerepel, ahol τ = L/R. Például egy 47 mH értékű kondenzátor 100 Ω értékű ellenálláson keresztüli táplálásakor az időtengely „1” értéke τ = L/R = 47*10^-3/100 = 470 μs. A 2 pedig közel 1 ezredmásodperc és így tovább.

A τ érték azért fontos, mert 1 τ idő alatt (τ = L/R) egy induktivitás a rákapcsolt feszültség hatására a maximális áramának 63%-át folyatja már át illetve amikor egy gerjesztett állapotban levő tekercset a kisütőellenállásra kapcsolunk, akkor 37%-ára esik τ idő alatt vissza. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-át éri el gerjesztéskor az áram, illetve kisütése esetén 5 τ idő alatt már csak 0,7 % marad a tekercsben. Tehát 5 τ idő alatt egy tekercs gyakorlatilag teljesen elveszti a tárolt energiáját.

Az induktivitás váltakozóáramú körben

<szamolo sor=4 jobb>L = 28,86 mikro;f = 7050 kilo;;X = 2*pi*f * L;</szamolo>

Az induktivitás látszólagos ellenállása adott frekvencián: [math]X_L = 2\pi \cdot f \cdot L = 6.283 \cdot f \cdot L[/math]

ahol

• X_L: a látszólagos ellenállás [Ω],
• L: az induktivitás [H] és
• f: a frekvencia [Hz].

Impedancia: [math]Z = j X_L = j 2\pi \cdot f \cdot L [ \Omega ][/math].

• Látszólagos ellenállást és impedanciát   frekvenciából és induktivitásból számoló.
• Induktivitást   frekvenciából és látszólagos ellenállásból vagy impedanciából számoló.
• Frekvenciát   induktivitásból és látszólagos ellenállásból vagy impedanciából számoló.