SNR
Signal-to-noise ratio - jel/zaj viszony.
SNR analóg áramköröknél
A jel/zaj viszonyt decibel-ben szokás megadni és azt adja meg, hogy mennyivel nagyobb a jel teljesítménye a zaj teljesítményéhez képest. Mivel a teljesítmény P = U2/R, ezért a feszültség négyzetével arányos. Logaritmikus skálán 2-szeres szorzóval számolandó.
[math]SNR = 10 \cdot lg \Bigg(\frac{P_{jel}}{P_{zaj}}\Bigg) = 20 \cdot log \Bigg(\frac{U_{jel RMS}}{U_{zaj RMS}}\Bigg)[/math]
- ahol
- RMS a négyzetes középérték (root mean square), azaz az effektív értéket jelöli.
SNR digitális modulációknál
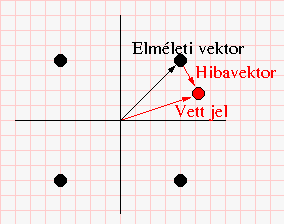
Digitális modulációk esetén precízebben számítható az SNR. Nézzünk például egy QPSK jel konstellációs diagramját. Kisugárzunk egy állapotot, azaz például a jobb felső sarokban levő helynek megfelelő jelet. Vételi oldalon a piros ponttal jelöltet sikerül detektálni.
Ekkor elmondható, hogy van egy jel nagyságunk (fekete nyíl) és egy ettől hibavektornyival eltérő vett jelünk - amely esetén már a fázishiba (időbeli elcsúszás) is formálisan mint amplitudóvektorral van jellemezve.
A fekete nyíl által jelölt elméleti vektor meghatározása a vétel során: az ehhez a konstellációs állapothoz tartozó kisugárzott tartalom vektorainak egyszerű vektorátlaga kiadja azt a pontot, ahova a zaj nélküli konstellációs pontnak esni kellene. Megjegyzendő, hogy az origóból kiinduló vektorok feszültséget jelképeznek, ami az A/D átalakítás során válik számértékké.
Azaz (I és Q komponensekkel leírva) az ugyanazon állapothoz tartozó elméleti vektor becslése az első legfontosabb művelet:
- [math]elmeletivektor_{I, Q} = \frac{1}{n}\sum_{n} vettjel_{I, Q}[/math]
Így az elemi hibából eredő SNR:
- [math]SNR = 10 \cdot lg \Big( \frac{elmeletivektor^2}{hibavektor^2} \Big) = 20 \cdot lg \Big(abs \Big(\frac{elmeletivektor}{hibavektor} \Big)\Big)[/math]
Ez túl sok, ezáltal nehezen értékelhető információt eredményezne, ezért inkább bizonyos időközönként (= bizonyos mintaszámonként), például másodpercenként próbáljuk egy skalár értékkel jellemezni az SNR-t. Azaz:
- [math]SNR_{atlag} = \frac{1}{n} \sum_{n} 10 \cdot lg \Big( \frac{elmeletivektor^2}{hibavektor^2} \Big) = \frac{1}{n} \sum_{n} 20 \cdot lg \Big(abs \Big(\frac{elmeletivektor}{hibavektor} \Big)\Big)[/math]
Ezen kívül diagnosztikai szempontból gyakran megkeresik az adott időegység alatt a minimum és maximum értékét is a pillanatnyi SNR értéknek.
Mivel a digitalizált jelet a feldolgozó algoritmus vektorként kezeli és a legközelebbi konstellációs ponthoz rendeli a demoduláció során, matematikailag alig jelent többlet számítást, hogy egyúttal folyamatosan SNR-t is számoljon. Ezért az ilyen vektormodulációknál az SNR mérése szinte minden esetben megvalósításra kerül és mint diagnosztikai információ, elérhető.