Modulációk sávszélesség igénye

Klasszikus modulációk

AM vagy más néven AM-DSB

AM-DSB a teljes neve, amely jelentése: amplitudómoduláció - kétoldalsávos (amplitude modulation - dual side band)

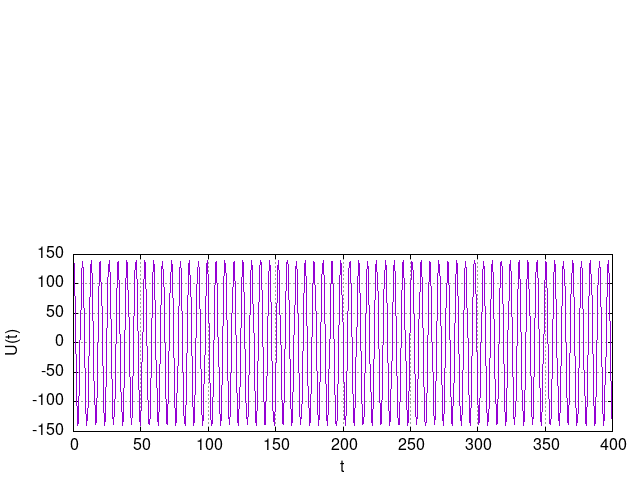
Amplitudómodulációt úgy képzelhetjük el, hogy a vivőt egy egységnyi DC offszetre szuperponált modulálójellel szorozzuk. Ezáltal a kapott termék a modulálójel pillanatnyi nullátmeneténél éppen a vivő, jelöljük U_v-vel. A modulálófeszültséget pedig jelöljük U_m-mel.

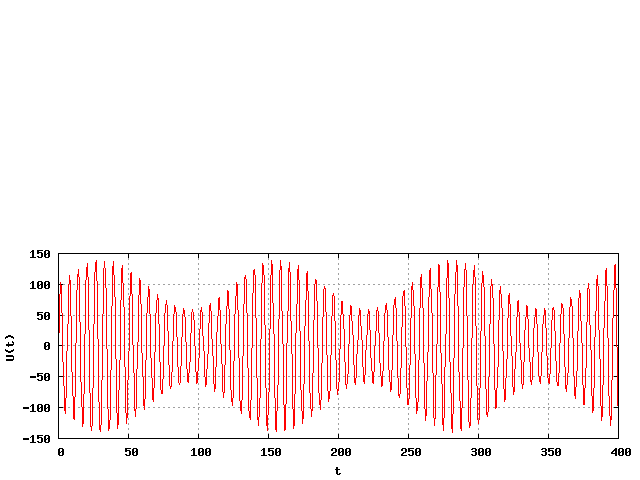
A fenti függvény: 100*cos(x) * (1 + 0.4*cos(x/20)) amely egyébként másképp felírva: 100*cos(x) + 40/2 * ( cos(x+x/20) + cos(x-x/20) )	AM vektorábrája
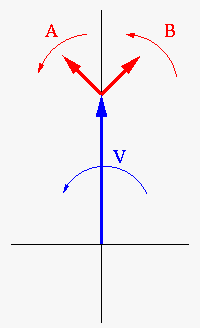
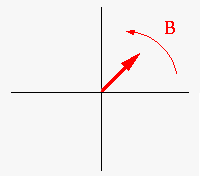
A vektorábrán a kék színű a vivő Uv amplitudóval (bal ábrán 100 egység). A modulálójel (kék) kettő darab Um/2 amplitudóra esik (bal ábra szerint 20 - 20 egység). A V forgónyíl a vivő frekvenciájának megfelelő forgási sebességű, az A forgónyíl a vivő és moduláló frekvencia összege, a B pedig a vivő és moduláló frekvencia különbségével forog.

Vezessünk be egy modulációs mélység paramétert. [math]m_a = \frac{U_m}{U_v}[/math].

A jel spektrumképe érdekesen alakul. Az egységnyi DC offsettel rendelkező szorzókeverés miatt lesz egy vivőnk és a moduláló jel frekvenciája különbségi és összegfrekvenciaként jelenik meg.

Sávszélesség igény

[math]BW = 2 \cdot f_{modmax}[/math]

ahol f_modmax a moduláló hang maximális frekvenciája

Energiák

P_v-vel jelöljük a vivő energiáját, amely feszültség négyzettel arányos. P_m-mel pedig a moduláló jel energiáját, amely szintén a moduláló jel feszültség négyzetével arányos.

A vivő energiája: [math]P_{vivo} = \frac{U_v^2}{2}[/math] A szorzókeverés melléktermékeként jelentkező oldalfrekvenciák energiája külön-külön: [math]P_{oldal} = \frac{U_m^2}{8}[/math] - és ez a vivőfrekvencia mindkét oldalán pontosan modulálófrekvencia távolságban jelen van.

AM-DSB/SC

AM-DSB - elnyomott vivővel (suppressed carrier)

Ezt úgy állíthatjuk elő, hogy vagy kiszűrjük a vivő frekvenciáját vagy ami egyszerűbb, kiegyenlített (DC offset nélküli) szorzókeveréssel állítjuk elő a jelet. Mellékesen megjegyezzük, hogy ilyen például a bPSK31 moduláció jele is. DC offszet nélküli, pusztán fázisváltást tartalmazó jel.

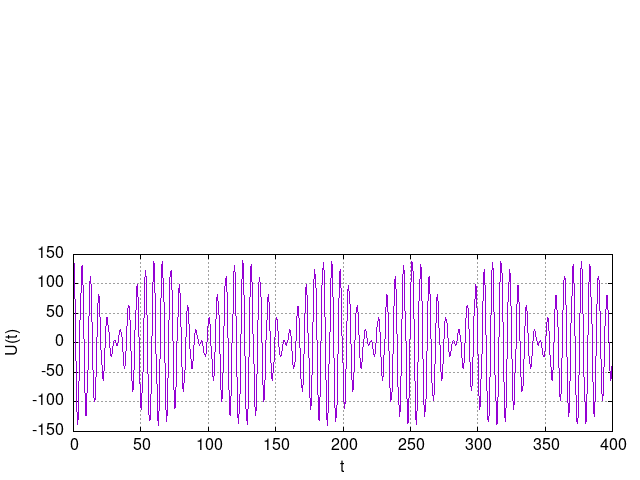
A fenti függvény: 140/2 * (cos( x + x/20) + cos(x - x/20))

AM-DSB/SC vektorábrája - a kék vivő NINCS

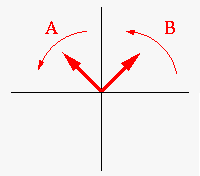
A modulálójel (piros) kettő darab Um/2 amplitudóra esik (bal ábra szerint 70 - 70 egység). Az A forgónyíl a képzeletbeli vivő és moduláló frekvencia összege, a B pedig a képzeletbeli vivő és moduláló frekvencia különbségével forog. Látható, hogy az előbbi 20-es értékű modulálóvektor helyett 70-es értékű modulálóvektort is képes kisugározni ugyanakkora amplitudó (~ teljesítményt) kisugárzására alkalmas adó. Ebből a példából talán látszik, hogy a vevő számára pusztán kényelmi célokat szolgáló vivő mekkora energiapazarlás.

Sávszélesség igény

megegyezik az AM-DSB jelével.

Energia terén az összes végfokozatból kijövő energia fele a felső oldalsávba, másik fele az alsó oldalsávba megy. Vivő, amely a vevőt segíti, jelen esetben hiányzik.

AM-SSB

SSB, mint egyoldalsávos (single side band)

Ez esetben például egy AM-DSB/SC jel nem kívánt oldalsávját szűréssel vagy egyéb technikával (Frekvenciafüggő fázistolás az egyik ágon és a végén jelösszegzés) elnyomjuk. Ekkor belátható, hogy a végfokozat tisztán az egyik oldalsáv energiáját fogja kisugározni.

A fenti függvény: 280/2 * cos(x - x/20) - a konstans szinuszos modulációnk jelenik meg a rádiófrekvenciára felkeverve az eddigi két oldalsáv pillanatnyi fázishelyzetük okán való erősítése vagy kioltódása helyett. Vagy az AM-hez képesti alapszintre való szuperponálódás helyett.

AM-SSB vektorábrája - a kék vivő NINCS, A oldalsáv NINCS

A modulálójel (piros) EGY darab Um/2 amplitudóval rendelkezik (bal ábra szerint 140 egység). A B forgónyíl a képzeletbeli vivő és moduláló frekvencia különbségével. Másszóval az alsó oldalsávról (LSB = lower side band) beszélünk éppen. Látható, hogy az AM esetén 20-as értékű modulálóvektor és a vivőelnyomás során 70-re emelt értékű modulálóvektor helyett 140-es értékűt is képes kisugározni ugyanakkora amplitudó (~ teljesítményt) kisugárzására alkalmas adó. Ebből a példából talán látszik, hogy ha csak egy oldalsávot sugárzunk, ugyan a vevő bonyolultabb lesz, de sok energia megspórolható. A digitális jelfeldolgozás ezt a problémát meghatározott időpillanatban és megfelelő frekvencián sugárzott referenciapontok megkeresésével energiatakarékos módon képes felderíteni és a korrekciókat pontosan elvégezni. Analóg esetben sajnos a pontos frekvencia megkeresése füllel történik. Ezáltal a beszélő szinte mindig magasabb vagy mélyebb tónusokkal hallatszik, mint a valódi hangja.

Sávszélesség igény

[math]BW = f_{modmax} - f_{modmin}[/math]

ahol f_modmax a moduláló hang maximális frekvenciája, f_{modmin} pedig a moduláló hang minimális frekvenciája. Igen kellemes megoldás, hiszen a rádiófrekvenciás spektrumban nem duplikáljuk a jelet. Időnként kisugárzott, a többi spektumvonalnál erősebb markerfrekvenciák segítségével lehet automatikusan ráhangolni a vevőt a pontos frekvenciára. Ez viszont feltételezi, hogy a vevő digitális jelfeldolgozással rendelkezik. Analóg megoldás ugyanis erre igen költséges lenne.

Érdekességként megemlítendő, hogy az SSB tulajdonképp egy alapsávi (mint például a hangfrekvencia) jel frekvencia-abszolutértékének felkeverése egy rádiófrekvenciás tartományba (vagy utólag a másik oldalsávot kiszűrjük). Ekkor egyébként felső oldalsávról (USB, upper side band) beszélünk. Ha a frekvencia-abszolutértékét negatív előjellel értelmezve keverjük fel (vagy a másik oldalsávot kiszűrjük keverés után), akkor alsó oldalsávról (LSB, lower side band) beszélünk.

Tehát az SSB felfogható egy például 300 Hz...2,7 kHz tartományban levő jel kisugárzásra alkalmas frekvenciára (például 14070,3 kHz...14072,7 kHz) történő áttevésére, amit vevő oldalon visszakeverünk 300 Hz...2,7 kHz közötti tartományra és igen kényelmes módon itt az alapsávon dolgozzuk fel a benne található információt.

FM

Frekvenciamoduláció esetén a moduláló jel amplitudójának pillanatnyi értékével arányos frekvenciát állítunk elő. Ergó a nagyobb pillanatnyi amplitudóhoz nagyobb frekvenciát rendelünk, a kisebb pillanatnyi amplitudóhoz kisebbet.

A fenti függvény: 100*cos( x + 10*cos(x/20))

FM vektorábrája (hasonló az AM vektorábrájához - csak más paraméterekkel)

A vektorábrán a kék színű a vivő Uv amplitudóval. Ennek a vivőnek a frekvenciáját moduláljuk. Azonban a modulálás következtében járulékosan „ráül” egy AM-nél már jól ismert bal és jobb oldalsáv. Így az AM-nél megismert - ám itt kevésbé kívánatos - oldalsávok szintén megjelennek. Ebből az is következik, hogyka kicsi a löket, akkor inkább AM jellegű az adásunk viselkedése, ha nagy a löket, akkor pedig a parazita „AM hatás” egyre inkább elhanyagolhatóvá válik, így egyre tisztább FM-et kapunk - de sokkal nagyobb RF sávszélességet „elpazarolva”

Vezessük be a frekvencialöket fogalmát, amely a vivőfrekvenciától való maximális eltérést jelenti a modulátorra fixen rákapcsolt maximális modulálófeszültség érték esetéen. Jelöljük f_D-vel.

frekvenciamodulációs tényező: [math]m_f = \frac{f_D}{f_{modmax}}[/math]

Sávszélesség igény

[math]BW = 2 \cdot \bigg(f_{modmax} + f_D + \sqrt{f_{modmax} \cdot f_D}\bigg)[/math]

Belátható, hogy zéró frekvencialöketnél AM jelleget hordoz a jel. Ha a löketet nagyon nagyra választjuk, akkor pedig az AM hatás elhanyagolható a számítás során. Speciális eset az NBFM-nél használt 1-es frekvenciamodulációs tényező, ahol a legnagyobb moduláló frekvenciával egyezik meg a frekvencialöket, így 2,1 kHz körül vágni célszerű a jelet, hogy a 12,5 kHz-es csatornába beleférjen az NBFM jelünk. Ez mint látszik, elég erőteljesen magán hordozza az AM jel vonásait is.

Műsorszórás terén hogy robusztusabb FM jelünk legyen, a frekvenciamodulációs tényezőt 5 környékére véve az AM jellet kezd elhanyagolhatóvá válni.

Érdekességként megemlítendő, hogy nem csak az FM rádióadás (amit FM vevőkészülékkel veszünk) FM adás, hanem az SSTV is, hiszen az adott képpont világosság-értékét az éppen kisugárzott frekvencia adja a vevőoldalon. Beleértve a fekete szintnél „feketébb” (azaz a feketénél is kisebb frekvencián adott) sor és képszinkron jelet is. Ekkor azonban a feldolgozónak DC csatoltnak kell lennie, hiszen a frekvencia értéke hordozza az információt és nem a frekvencia változás okozta váltakozóáramú jel - szemben azzal, amit például az analóg hang esetén megszoktunk.

PM

Fázismodulált átvitel esetén az állandó amplitúdójú vivő fázisa változik a moduláló jel amplitúdójának függvényében. Ha a periódusidőn belül változik a fázis, akkor a frekvencia is megváltozik. Fázis moduláció van akkor, ha a löket kicsi, ill. a periódusidő nagyobb a vivő periódusidejénél.

A fenti függvény: 140 * cos(x) * cos(x/20)	PM vektorábrája (amely hasonlít az AM-DSB/SC-re)
A PM jellege hasonlít az AM-DSB/SC-re. Azonban különbség az, hogy amíg az AM-DSB/SC mindkét oldalsávjában ugyanazt az információt kódoltuk (azaz az 'A' és 'B' vektorok hossza megegyezett), addig PM esetén a két oldalsáv egymáshoz képesti amplitudója változik.

Sávszélesség igény

AM-DSC/SC-vel megegyező: [math]BW = 2 \cdot \bigg(f_{modmax} + f_D + \sqrt{f_{modmax} \cdot f_D}\bigg)[/math]