Váltakozó áramú ellenállás

Elektromos áramköröket különféle paraméterekkel jellemzünk, amelyek között nagyon fontosak az elektromos paraméterek, például működési feszültség, áramfelvétel, fogyasztás, bemeneti impedancia, kimemeti impedancia (ha van kimenete) stb.

Mielőtt eljutnánk az impedancia magyarázatához, előtte érintőlegesen nézzünk meg néhány szükséges ismeretanyagot. A téma alapos megértéséhez feltétlenül szükséges a Komplex számábrázolás ismerete.

Ellenállás

Ha egy ellenállásokból álló áramkör két pontjára egyenfeszültséget kapcsolunk, akkor áram indul meg a körben. Az áramerősség nagyságát a két pont közötti eredő ellenállás határozza meg. Bővebben: Elektromos ellenállás szócikkben.

Jele: R

Mértékegysége: 1 Ω (1 Ohm)

Kiszámítása: [math]R = \frac{U_{=}}{I_{=}}[/math]

Ha ugyanerre a hálózatra váltakozó feszültséget kapcsolunk, akkor szintén igaz a fenti képlet. A feszültség és áram helyére írhatjuk a mennyiségek effektív értékét és csúcsértékét is. A hányados minden időpillanatban ugyanakkora lesz, mert a feszültség és az áramerősség fázisban van egymással.

Fásiban van: Például két szinuszos mennyiség azonos frekvenciájú és minden időpillanatban azonos fázishelyzetű.

[math]R = \frac{U_{~}}{I_{~}} = \frac{U_{eff}}{I_{eff}} = \frac{U_{cs}}{I_{cs}} [/math]

A φ fázisszög 0, mert a feszültség és az áram fázis-eltérése 0.

A fogyasztón fellépő teljesítmény csak hatásos teljesítmény: P = U₌*I₌=1/2 * U_{~ cs} * I_{~ cs} és [P] = W.

Reaktancia

Ha egy ideális tekercsre egyenfeszültséget kapcsolunk, akkor (állandósult állapotban) a tekercsen vágtelen nagy áram folyna, mert rövidzárként viselkedne.

Ideális tekercs: Csak induktivitása (L) van, az egyéb komponenseit elhanyagoljuk, tehát az egyenáramú ellenállása 0 ohm.

Állandósult állapot: A bekapcsolási jelenségek okozta átmeneti állapotok (tranziensek) lecsengése után állandósult értékek állnak be.

Ha egy ideális kondenzátorra egyenfeszültséget kapcsolunk, akkor (állandósult állapotban) a kondenzátoron nem folyna áram, mert szakadásként viselkedne.

Ideális kondenzátor: Csak kapacitása (C) van, az egyéb komponenseit elhanyagoljuk, tehát az egyenáramú ellenállása végtelen.

Ha azonban ezekre az energiatárolós elemekre (L, C) véges értékű váltakozó feszültséget kapcsolunk, akkor már másként viselkednek, azaz véges értékű váltakozó áram folyik át rajtuk.

A reaktancia jele: X Mértékegysége: 1 Ω (1 Ohm)

Az U_~ hatására a körben folyó áram: [math]I = \frac{U_{~}}{X_{~}}[/math]

A fogyasztón fellépő teljesítmény csak meddő teljesítményből áll (ami energiatárolást fejez ki). Q = U² / X és [Q]=var.

Induktív reaktancia: X_L

Tisztán induktív reaktanciája van az olyan körnek, amely csak (ideális) tekerecsekből áll.

X_L = j · 2πf · L = ω * L, ahol f a frekvencia, L az eredő induktivitás, ω a körfrekvencia, j a komplex képzetes rész jelölése.

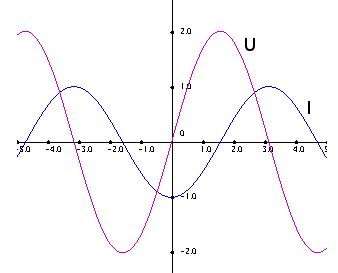
Fázisviszonyok: A feszültség siet φ = 90^o-ot az áramhoz képest. Ez a tekercs körüli mágneses erőtér felépülése miatt van.

Kapacitív reaktancia X_C

Tisztán kapacitív reaktanciája van az olyan körnek, amely csak (ideális) kondenzátorokból áll.

[math]X_c=\frac{1}{j 2\pi f C}[/math] = -j · 1/ ω · C, ahol f a frekvencia, C az eredő kapacitás, ω a körfrekvencia, j a komplex képzetes rész jelölése.

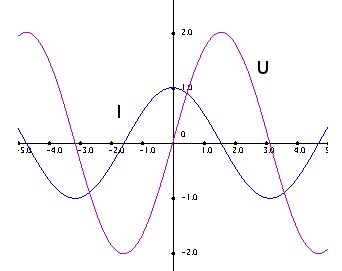
Fázisviszonyok: A feszültség késik φ = 90^o-ot az áramhoz képest. Csak a töltések fegyverzeten való felsorakozása után alakul kia teljes erőtér a kondenzátorban.

L-C körök reaktanciája

Ha egy áramkörben mindkét elem előfordul, akkor az eredő reaktancia az induktív és kapacitív eredő reaktanciák összege.

Egyszerű példa: Sorbakapcsolt L és C eredő reaktanciája: Ha X_L=j · 3 ohm és X_C = -j · 4 ohm, akkor az eredő reaktancia X=X_L+X_c=j · 3 - j · 4 = -j · 1 ohm.

Ilyenkor azt mondjuk, hogy a kör kapacitív jellegű, mert eredőben kapacitív reaktanciát tartalmaz. Ellenkező esetben induktív jellegűnek mondhatnánk.

Fázisviszonyok: Ilyenkor a φ fázisszög vagy +90^o vagy -90^o.

Impedancia

Ha olyan áramkörről beszélünk, amelyben egyszerre előfordul ellenállás és energiatároló elem (L és/vagy C), akkor a kört eredő impedanciájával tudjuk jellemezni.

Az impedancia jele: Z

Mértékegysége [Z] = 1 Ω (ohm)

Egy R-L, R-C vagy R-L-C kétpólus impedanciája a rákapcsolt feszültség effektív értékének és annak hatására meginduló áramerősség effektív értékének hányadosa: Z = U_eff/I_eff

Z = sqrt(R^2+X^2)

Fázisviszonyok: -90^o < φ < +90^o.

Vezetés jellegű mennyiségek

Vezetőképesség: G [G]=1 S(iemens) , G = 1/R

Szuszceptanica: A, [A]=1 S, A=1/X

Admittancia: Y, [Y]=1 S, Y=1/Z