Komplex számábrázolás

A hétköznapjainkban megszokott a valós számok használata. A valós számok alatt a pozitív és negatív egész és tört számok használatát értjük.

A komplex számok felhasználása

A komplex számok váltakozóáramú áramkörök (hangfrekvenciás, rádiófrekvenciás, ...) esetén kerülnek elő. Ugyanis a kapacitás és az induktivitás színuszos gerjesztés esetén a leg egyszerűbben úgy kezelhető, mint egy 90 fokkal eltolt impedanciájú építőelem.

Ebben az esetben - például egy soros RC kör vagy soros RL kör impedanciája az alább leírthoz hasonló komplex szám lesz, illetve az ilyen áramkör által felvett áram értéke is legegyszerűbben komplex számmal írható le.

Komplex számok

A komplex számok olyan rendezett párok, melyeknek elemei valós számok. Az egyik számot valós számként alkalmazzuk, a másik számot, amelyet matematikában [math]i[/math]-vel jelölünk, úgynevezett képzetes (imaginárius) szám. Egyéb speciális tulajdonsága az imaginárius tagnak, hogy a négyzetre emelve -1-et ad eredményül.

Az elektrotechnikában, tekintettel arra, hogy az i a váltakozó áramú áramerősséget is jelöli, ezért a j betűt alkalmazzuk helyette.

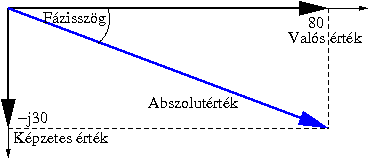
Példa egy komplex számra (például impedanciára):

Z = R + jX = 80 - j30 ohm

Ábrázolva:

A Z abszolut értéke: [math]|Z|=\sqrt{R^2+X^2}= \sqrt{80^2+(-30)^2}=\sqrt{6400+900}=85,44 \Omega[/math]

A fázistolás kiszámítása: [math]\varphi=arctg\frac{X}{R}=arctg\frac{-30}{80}=-20,55[/math]˚

Műveletek komplex számokkal

Összeadás: külön összeadjuk a valós értékeket és külön a képzetes értékeket.

Kivonás: ugyanaz mint az összeadás, csak kivonjuk összegzés helyett.

Szorzás: a j-s tagok egymással való szorzása: j*j=-1 -et eredményez. Ezáltal a

(R₁+jX₁) * (R₂+jX₂) = R₁*R₂+jX₁*jX₂+R₁*jX₂+jX₁*R₂ = R₁*R₂ - X₁*X₂ + j (R₁*X₂ + R₂*X₁)

Komplex számok exponenciális alakja

A számítások megkönnyítése érdekében gyakran áttérünk a komplex alakra.

Ekkor a fenti Z = 80 + j 30 felírható [math]Z = |Z| \cdot e^{j\varphi} = 85.44 \cdot e^{-j0,0363}[/math] formában is, amely annyit jelent, hogy

• abszolutértéke 85,44 ohm
• fázisszöge -0,0363 radián. [math]\varphi_{radian}=\frac{\pi}{180}\varphi_{fok}[/math], mivel 360 fok az éppen a [math]2\pi[/math] radián.
• valós értéke [math]R = |Z| * cos(\varphi)[/math]
• képzetes értéke: [math]X = |Z| * sin(\varphi)[/math]

Egyéb érdekességek

• Impedanciaillesztés méretezése esetén a meghajtó impedancia konjugáltja az ideális terhelés impedanciája. Például: Z_generátor = 50 + j30 ohm esetén egy Z_terhelés = 50 - j30 ohm adja a leg kedvezőbb eredményt, mivel a soros kapcsolás esetén a komplex tagok előjelesen összegződése éppen kiejti a komplex tagokat.