„Kondenzátor” változatai közötti eltérés
a (kisülés/feltöltés fix) |
(szócikk tömörítése) |
||
| 9. sor: | 9. sor: | ||
== A kapacitás alapfogalma == | == A kapacitás alapfogalma == | ||
| − | + | {| border="1" align="right" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| border="1" | ||
! Anyag !! Relatív permittivitás | ! Anyag !! Relatív permittivitás | ||
|- | |- | ||
| 40. sor: | 27. sor: | ||
|} | |} | ||
| − | = | + | <math>C = \varepsilon_0 \varepsilon_r \frac{A}{d}</math>, ahol a |
| + | |||
| + | ''C'' a kapacitás, mértékegysége a Farad (F)<br> | ||
| + | ''epszilon'' a permittivitás, ''epszilon<sub>0</sub>'' a vákum permittivitása, ''epszilon<sub>r</sub>'' pedig az adott anyag vákumhoz képesti szorzója<br> | ||
| + | ''A'' az egymással szemben álló ''fegyverzetek'' területe<br> | ||
| + | ''d'' a fegyverzetek közti távolság<br> | ||
| − | + | Vákum permittivitása: <math>\varepsilon_0 = 8.85*10^{-12} \frac{A s}{V m}</math> | |
| − | A | + | A témáról bővebben az [[elektromos mező]] című fejezetben. |
| − | + | == Kondenzátor egyenáramú körben == | |
| − | A kondenzátor | + | A kondenzátor által tárolt töltés: Q = C * U = I * t, azaz a kapacitás szorozva a kondenzátor feszültségével. Ugyanakkor úgy is felírhatjuk, hogy állandó töltő áramerősséget feltételezve a töltő áramerősség és az idő szorzata. Ebből az az is látható, hogy állandó áramerősséggel töltve egy kondenzátort, U = Q/C = I/C * t. Azaz az idő függvényében egyenletesen tesz szert nagyobb feszültségre, ahol a töltődés meredeksége az áramerősség és a kapacitás hányadosa. Természetesen ez megfordítva a kisütés folyamatára is érvényes. |
| − | + | Egy másik fontos tényező a kondenzátor által tárolt energia: <math>E=\frac{1}{2}CU^2</math>. | |
| − | < | + | A gyakorlatban legtöbbször nem állandó árammal töltődik a kondenzátor, hanem egy soros ellenálláson keresztül. A kondenzátor egy vele sorba kapcsolt ellenálláson történő feltöltése illetve egy párhuzamosan kapcsolt ellenálláson keresztüli kisütése exponenciális függvénnyel irható le. Ennek okát egyszerűen megérthetjük, ha arra gondolunk, hogy az üres kondenzátor feltöltésének kezdetekor az ellenállásra U<sub>t</sub> feszültség jut, amely árama I=U/R összefüggéssel kiszámítható, de például egy már félig feltöltött kondenzátor esetén a töltőáram már csak a fele értékű, azaz a töltési sebesség ezen pontban már csak a fele. |
| − | <gnuplot> | + | |
| − | set output ' | + | {| |
| + | |[[Kép:KondiFeltoltesKisutes_sch.png]] | ||
| + | |<gnuplot> | ||
| + | set output 'KondiFeltoltesKisutes.png' | ||
set size 1,1 | set size 1,1 | ||
set grid | set grid | ||
| − | set xlabel " | + | set ytics 0.1 |
| − | set ylabel " | + | set xlabel "Relatív idő" |
| − | + | set ylabel "Kondenzátor feszültsége" | |
| − | + | set size 1,0.5; | |
| − | set size 1 | + | plot [x=0:5] 1-exp(-x) title "töltéskor", exp(-x) title "kisütéskor" |
| − | |||
| − | plot [x= | ||
| − | |||
| − | |||
</gnuplot> | </gnuplot> | ||
| − | </ | + | |} |
| + | |||
| + | A fenti ábra idő és feszültségtengelye relatív. Az feszültség tengely „1” értéke az ellenálláson keresztül rákapcsolt feszültség értéke, az idő tengelyen úgynevezett τ érték szerepel, ahol τ = R * C. Például egy 100μF értékű kondenzátor 47 kΩ értékű ellenálláson keresztüli töltésekor az időtengely „1” értéke τ = R * C = 100*10<sup>-6</sup> * 47*10<sup>3</sup> = 4,7 másodperc. A 2 pedig a 9,4 másodperc és így tovább. | ||
| + | |||
| + | A τ érték azért fontos, mert 1 τ idő alatt (τ = R * C) egy kondenzátor 63%-ra töltődik illetve kisütéskor 37%-ára sül ki. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-ára tölthető fel, illetve kisütése esetén 5 τ idő alatt már csak 0,7 %-a marad a kondenzátorban. Tehát 5 τ idő alatt egy kondenzátor gyakorlatilag teljesen kisül. | ||
== Kondenzátor váltakozó áramú körben == | == Kondenzátor váltakozó áramú körben == | ||
| − | A kondenzátorra váltakozóáramú jelet kapcsolva látszólagos ellenállást mutat. Az értéke: | + | A kondenzátorra váltakozóáramú jelet kapcsolva látszólagos ellenállást mutat. Az értéke: <math>X_c=\frac{1}{2\pi f C}</math>, ahol f a frekvencia és C a kapacitás. Az X<sub>c</sub> pedig a képzetes ellenállás. |
| − | |||
| − | <math>X_c=\frac{1}{2\pi f C}</math>, ahol f a frekvencia és C a kapacitás. Az X<sub>c</sub> pedig a képzetes ellenállás. | ||
'''Példa:''' egy 10 nF -os kondenzátor 455 kHz-en mekkora képzetes ellenállást mutat? | '''Példa:''' egy 10 nF -os kondenzátor 455 kHz-en mekkora képzetes ellenállást mutat? | ||
A lap 2006. szeptember 22., 21:02-kori változata
Tartalomjegyzék
A kondenzátor feladata
- energiatárolás (rövidtávú)
- zajsimitás (váltakozóáramú komponensek csillapítása)
- egyenáramú komponens leválasztása
- induktivitással összekapcsolva rádiófrekvenciás frekvenciaszűrőt készíthetünk
- ellenállással összekapcsolva hangfrekvenciás szűrő készíthető
A kapacitás alapfogalma
| Anyag | Relatív permittivitás |
|---|---|
| Vákum: | 1 |
| Levegő | 1,00059 |
| Fém | 1 |
| Üveg | 5 .. 7 |
| Kerámia | 9,5 .. 100 |
| Desztillált víz | 81 |
| Báriumtitanát | 103 .. 104 |
[math]C = \varepsilon_0 \varepsilon_r \frac{A}{d}[/math], ahol a
C a kapacitás, mértékegysége a Farad (F)
epszilon a permittivitás, epszilon0 a vákum permittivitása, epszilonr pedig az adott anyag vákumhoz képesti szorzója
A az egymással szemben álló fegyverzetek területe
d a fegyverzetek közti távolság
Vákum permittivitása: [math]\varepsilon_0 = 8.85*10^{-12} \frac{A s}{V m}[/math]
A témáról bővebben az elektromos mező című fejezetben.
Kondenzátor egyenáramú körben
A kondenzátor által tárolt töltés: Q = C * U = I * t, azaz a kapacitás szorozva a kondenzátor feszültségével. Ugyanakkor úgy is felírhatjuk, hogy állandó töltő áramerősséget feltételezve a töltő áramerősség és az idő szorzata. Ebből az az is látható, hogy állandó áramerősséggel töltve egy kondenzátort, U = Q/C = I/C * t. Azaz az idő függvényében egyenletesen tesz szert nagyobb feszültségre, ahol a töltődés meredeksége az áramerősség és a kapacitás hányadosa. Természetesen ez megfordítva a kisütés folyamatára is érvényes.
Egy másik fontos tényező a kondenzátor által tárolt energia: [math]E=\frac{1}{2}CU^2[/math].
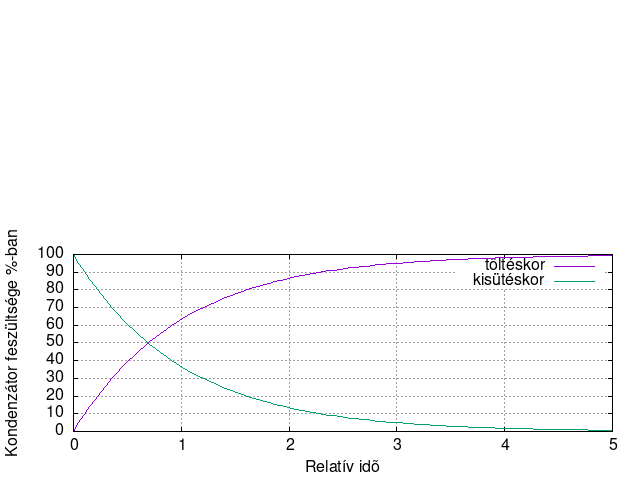
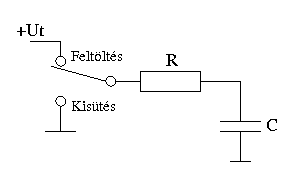
A gyakorlatban legtöbbször nem állandó árammal töltődik a kondenzátor, hanem egy soros ellenálláson keresztül. A kondenzátor egy vele sorba kapcsolt ellenálláson történő feltöltése illetve egy párhuzamosan kapcsolt ellenálláson keresztüli kisütése exponenciális függvénnyel irható le. Ennek okát egyszerűen megérthetjük, ha arra gondolunk, hogy az üres kondenzátor feltöltésének kezdetekor az ellenállásra Ut feszültség jut, amely árama I=U/R összefüggéssel kiszámítható, de például egy már félig feltöltött kondenzátor esetén a töltőáram már csak a fele értékű, azaz a töltési sebesség ezen pontban már csak a fele.
|
|
A fenti ábra idő és feszültségtengelye relatív. Az feszültség tengely „1” értéke az ellenálláson keresztül rákapcsolt feszültség értéke, az idő tengelyen úgynevezett τ érték szerepel, ahol τ = R * C. Például egy 100μF értékű kondenzátor 47 kΩ értékű ellenálláson keresztüli töltésekor az időtengely „1” értéke τ = R * C = 100*10-6 * 47*103 = 4,7 másodperc. A 2 pedig a 9,4 másodperc és így tovább.
A τ érték azért fontos, mert 1 τ idő alatt (τ = R * C) egy kondenzátor 63%-ra töltődik illetve kisütéskor 37%-ára sül ki. Ugyanakkor a másik jellegzetes érték az 5 τ, amely esetén 99,3%-ára tölthető fel, illetve kisütése esetén 5 τ idő alatt már csak 0,7 %-a marad a kondenzátorban. Tehát 5 τ idő alatt egy kondenzátor gyakorlatilag teljesen kisül.
Kondenzátor váltakozó áramú körben
A kondenzátorra váltakozóáramú jelet kapcsolva látszólagos ellenállást mutat. Az értéke: [math]X_c=\frac{1}{2\pi f C}[/math], ahol f a frekvencia és C a kapacitás. Az Xc pedig a képzetes ellenállás.
Példa: egy 10 nF -os kondenzátor 455 kHz-en mekkora képzetes ellenállást mutat?
Megoldás: [math]X_c=\frac{1}{2\pi f C} = \frac{1}{6.283*455*10^3*10*10^{-9}}= 34,98 \Omega[/math]