„Komplex számábrázolás” változatai közötti eltérés
a (komplex osztás) |
(Műveletek exponenciális alakkal) |
||
| 57. sor: | 57. sor: | ||
* valós értéke <math>R = |Z| * cos(\varphi)</math> | * valós értéke <math>R = |Z| * cos(\varphi)</math> | ||
* képzetes értéke: <math>X = |Z| * sin(\varphi)</math> | * képzetes értéke: <math>X = |Z| * sin(\varphi)</math> | ||
| + | |||
| + | == Műveletek az exponenciális alakkal == | ||
| + | |||
| + | * összeadás, kivonás: nehézkes - így ekkor inkább a fenti valós és képzetes értékes megoldást választjuk. | ||
| + | * szorzás: az abszolutértéket szorozzuk, a fázisszögeket pedig összegezzük. | ||
| + | <math>|Z_1| \cdot e^{j\varphi_1} \cdot |Z_2| \cdot e^{j\varphi_2} = |Z_1| \cdot |Z_2| \cdot e^{j(\varphi_1+\varphi_2)}</math> | ||
| + | * osztás: az abszolutértékeket osztjuk egymással, az osztandó fázisszügéből pedig kivonjuk az osztó fázisszögét. | ||
| + | <math>\frac{|Z_1| \cdot e^{j\varphi_1}}{|Z_2| \cdot e^{j\varphi_2}} = \frac{|Z_1|}{|Z_2|} \cdot e^{j(\varphi_1-\varphi_2)}</math> | ||
== Egyéb érdekességek == | == Egyéb érdekességek == | ||
A lap 2006. július 2., 21:46-kori változata
A hétköznapjainkban megszokott a valós számok használata. A valós számok alatt a pozitív és negatív egész és tört számok használatát értjük.
Tartalomjegyzék
A komplex számok felhasználása
Váltakozóáramú körökben, amelyekben van kondenzátor és/vagy induktivitás is, kerülnek elő a komplex számok. Ezen áramkörök esetében amennyiben az alább ismertetett komplex számokkal és komplex aritmetikai szabályokkal számolunk, használható az Ohm-törvény és a Kirchoff-törvények is.
Az eredményeket azonban szintén komplex számok formájában kapjuk meg. A legvégső számítás során azonban abszolutérték képzésével mégis egy olyan kézzelfogható például feszültség illetve áramértékhez jutunk, amelyet már közvetlenül műszerrel mérhetünk.
Az alább ismertetett fázistolást például oszcilloszkóp segítségével kimutathatjuk. Továbbá vannak olyan impedancia analizátorok, amelyek képesek komplex értékként kijelezni egy adott frekvencián az impedanciát.
Komplex számok
A komplex számok olyan rendezett párok, melyeknek elemei valós számok. Az egyik számot valós számként alkalmazzuk, a másik számot, amelyet matematikában [math]i[/math]-vel jelölünk, úgynevezett képzetes (imaginárius) szám. Egyéb speciális tulajdonsága az imaginárius tagnak, hogy a négyzetre emelve -1-et ad eredményül.
Az elektrotechnikában, tekintettel arra, hogy az i a váltakozó áramú áramerősséget is jelöli, ezért a j betűt alkalmazzuk helyette.
Példa egy komplex számra (például impedanciára):
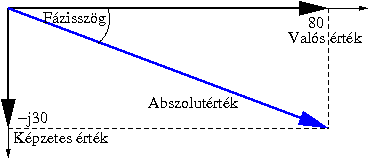
Z = R + jX = 80 - j30 ohm
Ábrázolva:
A Z abszolut értéke: [math]|Z|=\sqrt{R^2+X^2}= \sqrt{80^2+(-30)^2}=\sqrt{6400+900}=85,44 \Omega[/math]
A fázistolás kiszámítása: [math]\varphi=arctg\frac{X}{R}=arctg\frac{-30}{80}=-20,55[/math]˚
Műveletek komplex számokkal
Összeadás: külön összeadjuk a valós értékeket és külön a képzetes értékeket.
Kivonás: ugyanaz mint az összeadás, csak kivonjuk összegzés helyett.
Szorzás: a j-s tagok egymással való szorzása: j*j=-1 -et eredményez. Ezáltal a
(R1+jX1) * (R2+jX2) = R1*R2+jX1*jX2+R1*jX2+jX1*R2 = R1*R2 - X1*X2 + j (R1*X2 + R2*X1)
Osztás:
- A konjugált fogalma: egy komplex szám konjugáltjának hívjuk azt a számot, amely valós értéke ugyanaz, a képzetes értéke azonban ellenkező előjelű.
- Egy osztás során valós számmal tudunk csak osztani, így ha a nevezőben komplex érték van, akkor a számlálót és a nevezőt megszorozzuk a nevező konjugáltjával. Ekkor a nevezőben levó szorzást elvégezve meglátjuk, hogy a képzetes tagot eredményező vegyesszorzatok kiejtik egymást. Azaz
[math]\frac{R_1+jX_1}{R_2+jX_2}=\frac{(R_1+jX_1) \cdot (R_2-jX_2)}{(R_2+jX_2) \cdot (R_2-jX_2)} = \frac{R_1*R_2+X_1*X_2+j(R_2*X_1-R_1*X_2)}{{R_2}^2+{X_2}^2}[/math]
És ez így már tényleg könnyen elosztható, mivel a nevező tényleg egy valós szám lesz.
Komplex számok exponenciális alakja
A számítások megkönnyítése érdekében gyakran áttérünk a komplex alakra.
Ekkor a fenti Z = 80 + j 30 felírható [math]Z = |Z| \cdot e^{j\varphi} = 85.44 \cdot e^{-j0,0363}[/math] formában is, amely annyit jelent, hogy
- abszolutértéke 85,44 ohm
- fázisszöge -0,0363 radián. [math]\varphi_{radian}=\frac{\pi}{180}\varphi_{fok}[/math], mivel 360 fok az éppen a [math]2\pi[/math] radián.
- valós értéke [math]R = |Z| * cos(\varphi)[/math]
- képzetes értéke: [math]X = |Z| * sin(\varphi)[/math]
Műveletek az exponenciális alakkal
- összeadás, kivonás: nehézkes - így ekkor inkább a fenti valós és képzetes értékes megoldást választjuk.
- szorzás: az abszolutértéket szorozzuk, a fázisszögeket pedig összegezzük.
[math]|Z_1| \cdot e^{j\varphi_1} \cdot |Z_2| \cdot e^{j\varphi_2} = |Z_1| \cdot |Z_2| \cdot e^{j(\varphi_1+\varphi_2)}[/math]
- osztás: az abszolutértékeket osztjuk egymással, az osztandó fázisszügéből pedig kivonjuk az osztó fázisszögét.
[math]\frac{|Z_1| \cdot e^{j\varphi_1}}{|Z_2| \cdot e^{j\varphi_2}} = \frac{|Z_1|}{|Z_2|} \cdot e^{j(\varphi_1-\varphi_2)}[/math]
Egyéb érdekességek
- Impedanciaillesztés méretezése esetén a meghajtó impedancia konjugáltja az ideális terhelés impedanciája. Például: Zgenerátor = 50 + j30 ohm esetén egy Zterhelés = 50 - j30 ohm adja a leg kedvezőbb eredményt, mivel a soros kapcsolás esetén a komplex tagok előjelesen összegződése éppen kiejti a komplex tagokat.