„Transzformátor” változatai közötti eltérés
a |
|||
| 71. sor: | 71. sor: | ||
=== ... feszülségátalakítóként === | === ... feszülségátalakítóként === | ||
| + | |||
| + | Ideális, kis veszteségű transzformátor esetén: | ||
| + | |||
| + | :<math>U_{ki} = U_{be} \cdot \frac{N_{ki}}{N_{be}}</math> | ||
| + | |||
| + | ;ahol: | ||
| + | * N<sub>be</sub>: primer tekercs menetszáma, ahova U<sub>be</sub> lesz kapcsolva | ||
| + | * N<sub>ki</sub>: szekunder tekercs menetszáma, ahonnan U<sub>ki</sub> feszültséget kívánjuk kicsatolni. | ||
=== ... áramerősség átalakítóként === | === ... áramerősség átalakítóként === | ||
| + | |||
| + | Ideális, kis veszteségű transzformátor esetén: | ||
| + | |||
| + | :<math>I_{mero} = I_{foag} \cdot \frac{N_{foag}}{N_{mero}}</math> | ||
| + | |||
| + | ;ahol: | ||
| + | * N<sub>főág</sub>: primer tekercs menetszáma, ahova I<sub>főág</sub> árama lesz kapcsolva | ||
| + | * N<sub>mérő</sub>: szekunder tekercs menetszáma, ahonnan I<sub>mérő</sub> mérőági áramerősséget kívánjuk kicsatolni. | ||
| + | |||
| + | Érdemes megfigyelni, hogy a feltranszformálás során jutunk kisebb áramerősséghez. | ||
=== ... impedancia átalakítóként === | === ... impedancia átalakítóként === | ||
| + | |||
| + | Ideális, kis veszteségű transzformátor esetén: | ||
| + | |||
| + | :<math>Z_{ki} = Z_{be} \cdot \Bigg(\frac{N_{ki}}{N_{be}}\Bigg)^2</math> | ||
| + | |||
| + | ;ahol: | ||
| + | * N<sub>be</sub>: primer tekercs menetszáma, ahova Z<sub>be</sub> impedacia lesz kapcsolva | ||
| + | * N<sub>ki</sub>: szekunder tekercs menetszáma, ahonnan Z<sub>ki</sub> impedancián kívánunk kicsatolni. | ||
=== ... leválasztó transzformátorként === | === ... leválasztó transzformátorként === | ||
| + | |||
| + | A fentiek szerint, ahonban okvetlenül galvanikusan nem érintkező primer és szekunder tekerccsel. | ||
=== ... szimmetrizáló transzformátorként === | === ... szimmetrizáló transzformátorként === | ||
| + | Ennek kétféle módszere ismert: | ||
| + | * azonos primer és szekunder menetszámú leválasztó transzformátor, amely szekunder ága földfüggetlen. | ||
| + | * vagy autotrafóként képzeljünk el egy 5 kivezetéses induktivitást, amely közepére kötjük a földet, egyik végére a meleg eret. A földszimmetrikus kivezetést pedig a | ||
| + | ** föld és melegér közt a fele menetszámnál csatoljuk ki | ||
| + | ** másik felét pedig ugyanekkora menetszámmal a tekercsközép túloldalán. | ||
| + | ** (a tuloldali végen levő tekercsrész elhagyható, csak a szemléletesség kedvéért lett így elképzelve) | ||
[[Kategória:Elektronikai alkatrészek]] [[Kategória: Passzív alkatrészek]] | [[Kategória:Elektronikai alkatrészek]] [[Kategória: Passzív alkatrészek]] | ||
A lap jelenlegi, 2010. július 19., 13:26-kori változata
Transzformátort sok célra használunk: feszültség átalakításra, leválasztásra, impedancia átalakításra, szimmetrizálásra, ...
Tartalomjegyzék
A transzformátor rövid története
A transzformátor felépítése
Az egyfázisú transzformátor két, csatolásban lévő tekercsből áll. A csatolás azt jelenti, hogy az egyik tekercs által gerjesztett mágneses erővonalak egy része áthalad a másik tekercsen. A csatolás mértékének növelése érdekében a két tekercset egymásra helyezik és vasmagra helyezik őket. A tekercsek rézből készülnek, a jó villamos vezetőképesség miatt. A vasmag jó mágneses tulajdonságokkal rendelkező anyag, nagy relatív permeabilitású.
A vasmag kialakítása alapján nevezik az efféle „áram-átalakítókat” köpeny, lánc illetve toroid típusú transzformátoroknak.
A háromfázisú transzformátorok tulajdonképpen három darab egyfázisú transzformátorból állnak. A három tekercs csillag vagy delta kapcsolásban van összekötve.
A transzformátor működése
Az egyfázisú transzformátor egyik tekercsére szinuszos, váltakozó feszültséget kapcsolva a tekercsben áram indul meg. Ezt a tekercset primer oldali tekercsnek nevezzük. A primer tekercs árama mágneses teret gerjeszt a tekercs belsejében. Ennek a térnek az erővonalai metszik a másik tekercset, így abban feszültség indukálódik. Ez a tekercs a szekunder tekercs. Ha a szekunder körre fogyasztót kapcsolunk, akkor áram indul meg a körben olyan irányban, hogy a szekunder áram által keltett mágneses tér - a Lenz-törvény értelmében - csillapítani igyekszik az őt létrehozó hatást, azaz a primer áramot. Ezért ha jobban megterheljük a szekunder oldalt, a primer oldal árama is növekedni fog, hogy a vasmagban lévő fluxust fenn tudja tartani.
Legyen a primer oldali tekercs N1 menetszámú, a szekunder oldali N2 menetszámú. Ekkor az alábbiak érvényesek:
- A transzformátor menetszám-áttétele: a = N1/N2
- A primer feszültség U1, a szekunder U2.
- Az ideális (veszteségmentes) transzformátor feszültség-áttétele megegyezik a menetszám-áttételével: a= U1/U2 = N1/N2
- Az áramáttétel ezzel szemben: a= N1/N2 = I2/I1.
- Veszteségmentes transzformátor esetén a primer oldalon bemenő teljesítmény megegyezik a szekunder oldalon kivehető teljesítménnyel: P1 = P2.
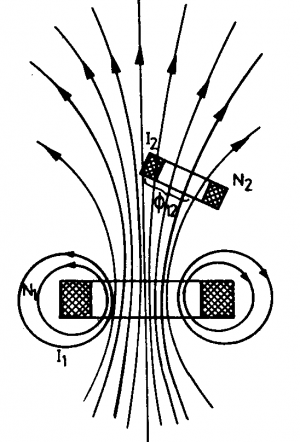
Kölcsönös indukció
Legyen az 1-es, N1 menetszámú tekercs mágneses terében a 2-es ( N2 ) tekercs. Ekkor 2-es tekercsen Φ12 fluxusrész halad át. Ha az 1-es tekercsen átfolyó I1 áram megváltozik, akkor a Φ12 fluxus is. Ekkor 2-es tekercsben Ui feszültség indukálódik.
[math]U_i = N_2 \cdot \frac{\Delta \Phi_{12}}{\Delta t}[/math]
A 2-es tekercsben indukált feszültség az Ii áramnak az időegység alatti változásával arányos.
[math]U_i = M_{12} \cdot \frac{\Delta I}{\Delta t}[/math]
Az M12 kölcsönös indukciós tényező azt fejezi ki, hogy egy tekercs áramának 1 másodperc alatt 1 amperrel való egyenletes megváltozása a másik, nyitott kapcsú tekercsben hány volt feszültséget indukál. Mértékegysége a henry.
A transzformátorok veszteségei
A nem ideális transzformátor veszteségekkel üzemel. A betáplált teljesítményből levonva a veszteségeket kapjuk a kivehető teljesítményt. A primer és szekunder tekercsek jó villamos vezetőképességű anyagból készülnek, de mégis van ellenállásuk. A tekercseken átfolyó áram Pt = I2 * R tekercsveszteséget hoz létre, amely a rézhuzalt melegíti. Mivel ez mindkét oldalon jelentkezik, így beszélhetünk primer és szekunder tekercsveszteségről. A vasmagban is keletkezik veszteség. Mivel a transzformátort általában váltakozó feszültséggel tápláljuk, a vasmag mágnesezettségének iránya is váltakozik, periódusonként kétszer. Mivel a vas átmágnesezéséhez energia kell, így ez is veszteségként jelentkezik, amely a primer feszültség négyzetével arányos mennyiség. Az átmágnesezési - vagy hiszterézis - veszteséget úgy lehet csökkenteni, ha jobb relatív permeabilitású anyagot használunk a transzformátorban.
A vasmagban is indukálódik feszültség, mivel változó mágneses térben van. Ráadásul a vas jó villamos vezetőképességű anyag, így a belső feszültségek hatására ún. örvényáramok indulnak meg benne, amik a vas ellenállása miatt szintén melegítik a transzformátort és veszteségként jelentkeznek. Ezt a hatást úgy lehet csökkenteni, ha a vasmagot vaslemezekből állítjuk össze, így a lemezek közötti ellenállás megnövekszik és kisebb áramok tudnak kialakulni. Nagyon jó módszer a porkohászati úton előállított „vasmagok” alkalmazása, hiszen ezekben minimális az örvényáramú veszteség.
A transzformátorok üzemállapotai
Üresjárási üzemállapot: Ha a transzformátor primer tekercsére névleges feszültséget kapcsolunk és a szekunder kapcsokon végtelen ellenállás van (I2 = 0, azaz nincs terhelés), akkor a transzformátor üresjárási üzemállapotban van. Ilyenkor a következő megállapítások érvényesek:
- R2=végtelen //azaz nincs terhelés, a kimeneten szakadás van
- U1=Unévleges // mert ezt kapcsoltuk rá
- I1 = I0(vagy Iüj), ahol I0 az üresjárási áram
- U2 = U2max //a szekunder feszültség maximuma mérhető
- I2 = 0
- P1 = Püj = Pvas //a felvett teljesítmény legnagyobb részét a vasveszteség adja
Rövidzárási üzemállapot: A transzformátor szekunder kapcsait rövidre zárjuk. A primer tekercsekre akkora feszültséget kapcsolunk, hogy Inévleges áram induljon meg. A következő megállapításokat tehetjük:
- R2=0 //azaz maximális a terhelés, a kimeneten rövidzár van
- I1 = IRZ(rövidzárási áram)
- U2=0 // ez is egyértelmű...
- I2 = I2max //a szekunder áram maximuma mérhető
- U1 = URZ //a névleges feszültség töredéke
- P1 = PRZ = Pt //a felvett teljesítmény legnagyobb részét a tekercsveszteségek adják
- Drop [epszilon] = Százalékos rövidzárási feszültségesés. ((IRZ/In)*100%)
Terhelési állapot: A két szélsőség között...folyt köv.
A transzformátorok csoportosítása
Felhasználása
... feszülségátalakítóként
Ideális, kis veszteségű transzformátor esetén:
- [math]U_{ki} = U_{be} \cdot \frac{N_{ki}}{N_{be}}[/math]
- ahol
- Nbe: primer tekercs menetszáma, ahova Ube lesz kapcsolva
- Nki: szekunder tekercs menetszáma, ahonnan Uki feszültséget kívánjuk kicsatolni.
... áramerősség átalakítóként
Ideális, kis veszteségű transzformátor esetén:
- [math]I_{mero} = I_{foag} \cdot \frac{N_{foag}}{N_{mero}}[/math]
- ahol
- Nfőág: primer tekercs menetszáma, ahova Ifőág árama lesz kapcsolva
- Nmérő: szekunder tekercs menetszáma, ahonnan Imérő mérőági áramerősséget kívánjuk kicsatolni.
Érdemes megfigyelni, hogy a feltranszformálás során jutunk kisebb áramerősséghez.
... impedancia átalakítóként
Ideális, kis veszteségű transzformátor esetén:
- [math]Z_{ki} = Z_{be} \cdot \Bigg(\frac{N_{ki}}{N_{be}}\Bigg)^2[/math]
- ahol
- Nbe: primer tekercs menetszáma, ahova Zbe impedacia lesz kapcsolva
- Nki: szekunder tekercs menetszáma, ahonnan Zki impedancián kívánunk kicsatolni.
... leválasztó transzformátorként
A fentiek szerint, ahonban okvetlenül galvanikusan nem érintkező primer és szekunder tekerccsel.
... szimmetrizáló transzformátorként
Ennek kétféle módszere ismert:
- azonos primer és szekunder menetszámú leválasztó transzformátor, amely szekunder ága földfüggetlen.
- vagy autotrafóként képzeljünk el egy 5 kivezetéses induktivitást, amely közepére kötjük a földet, egyik végére a meleg eret. A földszimmetrikus kivezetést pedig a
- föld és melegér közt a fele menetszámnál csatoljuk ki
- másik felét pedig ugyanekkora menetszámmal a tekercsközép túloldalán.
- (a tuloldali végen levő tekercsrész elhagyható, csak a szemléletesség kedvéért lett így elképzelve)