Fourier transzformáció

Egy időben változó jel előállítható különböző freknvenciájú, fázisú és amplitúdójú jelek összegeként. A Fourier-transzformáció az a művelet, amely egy adott jelhez megadja ezt a felbontást. A Fourier-transzformáció inverze szolgál arra, hogy a frekvencia spektrumból (frekvenciatartomány) megadja az időfüggő jelet (időtartomány).

A Fourier-transzformáció ismerete alapvető fontosságú a lineáris rendszerek tulajdonságainak vizsgálatához. Mivel az áramkörök jelentős része frekvenciafüggő jelleget mutat, ezért a frekvenciatartománybeli viselkedés sokszor könnyebben leírható, mint az időtartománybeli.

A Fourier-transzformáció felhasználása

Egy fontos alkalmazás különféle transzformációk elvégezése a jelen.

Például: egy négyszögjelből lehet-e kis torzítású színuszjelet csinálni?

Igen. A négyszögjel Fourier-sora [math]f(t)=\frac{4}{\pi}\Big( \sin(\omega t)+\frac{1}{3}\sin(3\omega t)+\frac{1}{5}\sin(5\omega t)+\frac{1}{7}\sin(7\omega t)+\dots \Big)[/math]

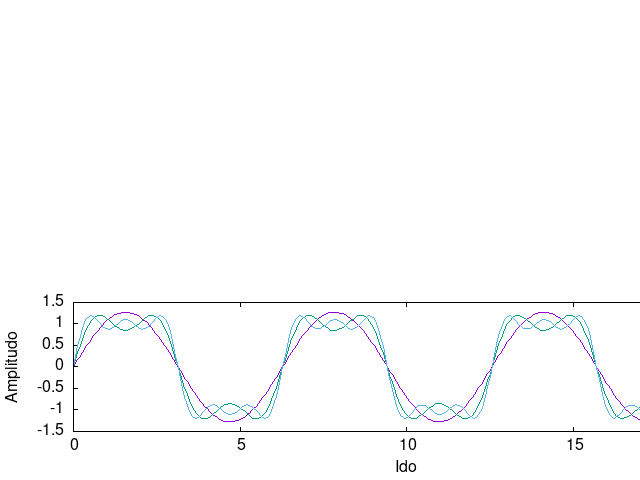
A fenti Fourier sorból és a mellékelt ábrából látható, amennyiben beépítünk a jelútba egy olyan aluláteresztő szűrőt, amely a négyszögjel alapfrekvenciájának 3-szorosát már nem engedi át, akkor színuszjelet kapunk.

További érdekes alkalmazása a szűrések és kiemelések. Azaz például egy hangfrekvenciás jelből egy sípolást el szeretnénk nyomni, vagy pedig egy bizonyos frekvenciatartományt fel szeretnénk hangosítani.

Rádiófrekvenciás jel esetén a Fourier transzformáció legfontosabb alkalmazása az OFDM jel demodulálása során kerül előtérbe, ahol a sok vivőfrekvenciát nem sok digitális szűrővel választjuk szét, hanem egyetlen Fourier transzformációval.

Folytonos Fourier transzformáció

Egy jel Fourier transzformáltja az a jel, amin ha elvégezzük az alább látható inverz-Fourier transzformációt, visszakapjuk a jelet:

[math]f \left( t \right) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty F\left(j\omega\right) e^{j\omega t}\,d\omega[/math]

Tehát a Fourier transzformáció:

[math]F \left( j\omega \right) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty f\left( t \right) e^{-j\omega t}\,dt[/math]

Ha már ilyen szép integráloknál tartunk, fontos megemliteni, hogy ez csak akkor végezhető el, ha a jel abszolút vagy négyzetesen integrálható. Tehát véges az energiatartalma. Megjegyzés: nem véges energiatartalmú jeleknek is létezhet Fourier transzformáltja, de azt nem ezzel az integrállal kell előállitani.

A fenti összefüggésnél a [math]e^{j\omega t}=\cos(\omega t)+j \cdot \sin(\omega t)[/math], az [math]|F\left(j \omega\right)|[/math] az amplitudóspektrum, az [math]arc(F(j\omega))[/math] pedig a fázisspektrum.

A Fourier transzformált előállitására egy kellemesebb módszer azt egy táblázatból kikeresni. Ebben az angol nyelvű wikipedia egy cikke nagyon hasznos segitségnek bizonyult. Ugyanitt vannak táblázatba foglalva a Fourier transzformáció azonosságai.

Diszkrét Fourier Transzformáció (DFT)

Az előző részben ismertetett folytonos Fourier transzformáció szép, azonban a gyakorlatban, mivel diszkrét idejű jelekkel dolgozunk, a transzformációt is ennek megfelelően egyszerűsítjük. Az alábbi összefüggéssel tehát az elemi színuszos komponensek számíthatóak ki.

[math]X[k] = \sum_{n=0}^{N-1} x[n] \,e^{-j 2 \pi \frac{k}{N} n}[/math]

A jelet pedig visszaállíthatjuk az egyes színuszos oszcillátorok jeleinek összegeként:

[math]x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] e^{j 2 \pi \frac{k}{N} n} \quad \quad n = 0, 1, \dots, N-1 \,[/math]

Fast Fourier Transformáció (FFT)

A gyors Fourier transzformáció eredménye egyezik a fenti DFT eredményével, azonban a művelethez szükséges idő nem N², hanem N*log(N), ami például egy 1024 pontos transzformációnál 300-szor gyorsabb számítást jelent.

Az FFT egyetlen korlátja, hogy a pontszám nem lehet tetszőleges, például nem lehet 1000 pontos, csak 2 valamely hatványa lehet. Azonban az említett sebességnövekedés miatt ezt a kompromisszumot elfogadjuk.

FFT megvalósítása

FFT-t kétféleképpen csinálhatunk. Vagy letöltjük a http://www.fftw.org -ról az FFT függvénykönyvtárat, vagy saját magunk írunk egy FFT algoritmust.

Az alábbiakban egy rádióamatőr célokra igen jól felhasználható FFT számító példa kerül ismertetésre.

-- folyt köv --