„Soros és párhuzamos kapcsolás” változatai közötti eltérés
(+= erősítők + formázás) |
|||
| 4. sor: | 4. sor: | ||
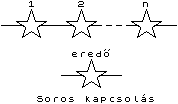
== Ellenállások soros kapcsolása == | == Ellenállások soros kapcsolása == | ||
| − | Soros kapcsolás esetén az eredő ellenállás az egyes [[elektromos ellenállás|ellenállás]]ok összege. Azaz | + | Soros kapcsolás esetén az eredő ellenállás az egyes [[elektromos ellenállás|ellenállás]]ok összege. Azaz <br> |
| − | |||
<math>R_{soros} = R_{1} + R_{2} + \dots + R_{n}</math> | <math>R_{soros} = R_{1} + R_{2} + \dots + R_{n}</math> | ||
| − | Az ellenálláson eső feszültség soros kapcsolás esetén: <math>U_{R_{kiszemelt}} = U_{be} \cdot \frac{R_{kiszemelt}}{R_{soros}}</math>, ahol U<sub>be</sub> a tápfeszültség, R<sub>kiszemelt</sub> amin akarom tudni, R<sub>soros</sub> pedig a fent számított eredő ellenállás. Érdemes megjegyezni, hogy az így kiszámított elemi feszültségek összege éppen a bemenő feszültséget kell hogy adja. | + | Az ellenálláson eső feszültség soros kapcsolás esetén: <br> |
| + | <math>U_{R_{kiszemelt}} = U_{be} \cdot \frac{R_{kiszemelt}}{R_{soros}}</math>, ahol | ||
| + | * U<sub>be</sub> a tápfeszültség, | ||
| + | * R<sub>kiszemelt</sub> amin akarom tudni, | ||
| + | * R<sub>soros</sub> pedig a fent számított eredő ellenállás. | ||
| + | Érdemes megjegyezni, hogy az így kiszámított elemi feszültségek összege éppen a bemenő feszültséget kell hogy adja. | ||
| − | Az ellenálláson átfolyó áram: <math>I = \frac{U_{be}}{R_{soros}}</math> Soros kapcsolás esetén minden komponens árama ugyanakkora. | + | Az ellenálláson átfolyó áram: <br> |
| − | + | <math>I = \frac{U_{be}}{R_{soros}}</math> <br> | |
| − | + | Soros kapcsolás esetén minden komponens árama ugyanakkora. | |
| + | [[Elektromos vezetés]]sel kifejezve: <br> | ||
<math>G_{soros} = \frac{1}{\frac{1}{G_1} + \frac{1}{G_2} + \dots + \frac{1}{G_n}}</math> | <math>G_{soros} = \frac{1}{\frac{1}{G_1} + \frac{1}{G_2} + \dots + \frac{1}{G_n}}</math> | ||
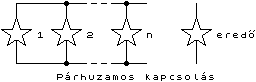
== Ellenállások párhuzamos kapcsolása == | == Ellenállások párhuzamos kapcsolása == | ||
| − | Párhuzamos kapcsolás esetén a az eredő [[elektromos vezetés|vezetés]] az egyes [[elektromos ellenállás|ellenállás]]ok vezetésének összege. Mivel a vezetés az ellenállás reciproka (1/R), ezért | + | Párhuzamos kapcsolás esetén a az eredő [[elektromos vezetés|vezetés]] az egyes [[elektromos ellenállás|ellenállás]]ok vezetésének összege. Mivel a vezetés az ellenállás reciproka (1/R), ezért <br> |
| − | |||
<math>R_{parhuzamos} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}}</math> | <math>R_{parhuzamos} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}}</math> | ||
Az ellenállásokon eső feszültség: tekintettel arra, hogy mindegyik ugyanoda van kötve, ezért megegyezik. | Az ellenállásokon eső feszültség: tekintettel arra, hogy mindegyik ugyanoda van kötve, ezért megegyezik. | ||
| − | Az ellenállásokon átfolyó áram: <math>I = U_{be} \cdot \frac{\frac{1}{R_{kiszemelt}}}{\frac{1}{R_{parhuzamos}}} = U_{be} \cdot \frac{R_{parhuzamos}}{R_{kiszemelt}}</math> | + | Az ellenállásokon átfolyó áram: <br> |
| + | <math>I = U_{be} \cdot \frac{\frac{1}{R_{kiszemelt}}}{\frac{1}{R_{parhuzamos}}} = U_{be} \cdot \frac{R_{parhuzamos}}{R_{kiszemelt}}</math>. | ||
| − | + | Az áramok összege pedig a tápláló áram. | |
| + | [[Elektromos vezetés]]sel kifejezve: <br> | ||
<math>G_{parhuzamos} = G_{1} + G_{2} + \dots + G_{n}</math> | <math>G_{parhuzamos} = G_{1} + G_{2} + \dots + G_{n}</math> | ||
| 44. sor: | 50. sor: | ||
== Induktivitások soros kapcsolása == | == Induktivitások soros kapcsolása == | ||
| − | Ha az [[induktivitás]]ok között nincs csatolás: <math>L_{soros} = L_1 + L_2 + \dots + L_n</math> | + | Ha az [[induktivitás]]ok között nincs csatolás: <br> |
| + | <math>L_{soros} = L_1 + L_2 + \dots + L_n</math> | ||
| − | Két, csatolásban lévő induktivitás esetén: <math>L_{soros} = L_1 + L_2 + 2*M</math>, ahol M a kölcsönös induktivitás. | + | Két, csatolásban lévő induktivitás esetén: <br> |
| + | <math>L_{soros} = L_1 + L_2 + 2*M</math>, ahol <br> | ||
| + | * M a kölcsönös induktivitás. | ||
== Induktivitások párhuzamos kapcsolása == | == Induktivitások párhuzamos kapcsolása == | ||
| − | Ha az induktivitások között nincs csatolás: <math>L_{parhuzamos} = \frac{1}{\frac{1}{L_1} + \frac{1}{L_2} + \dots + \frac{1}{L_n}}</math> | + | Ha az induktivitások között nincs csatolás: <br> |
| + | <math>L_{parhuzamos} = \frac{1}{\frac{1}{L_1} + \frac{1}{L_2} + \dots + \frac{1}{L_n}}</math> | ||
| − | Két, csatolásban lévő induktivitás esetén: <math>L = \frac{L_1 \cdot L_2 - M^2}{L_1 + L_ 2 - M}</math>, ahol M a kölcsönös induktivitás. | + | Két, csatolásban lévő induktivitás esetén: <br> |
| + | <math>L = \frac{L_1 \cdot L_2 - M^2}{L_1 + L_ 2 - M}</math>, ahol <br> | ||
| + | * M a kölcsönös induktivitás. | ||
= LC és RLC tagok = | = LC és RLC tagok = | ||
| 59. sor: | 71. sor: | ||
A [[kapacitás]] reaktanciáját X<sub>C</sub>, az [[induktivitás]]ét X<sub>L</sub> -lel jelöljük. | A [[kapacitás]] reaktanciáját X<sub>C</sub>, az [[induktivitás]]ét X<sub>L</sub> -lel jelöljük. | ||
| − | '''Soros kapcsolásuk:''' <math>X_{soros} = X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} )</math> | + | '''Soros kapcsolásuk:''' <br> |
| + | <math>X_{soros} = X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} )</math> | ||
| − | '''Párhuzamos kapcsolásuk: <math>X_{parhuzamos} = \frac{1}{ \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) }</math> | + | '''Párhuzamos kapcsolásuk:''' <br> |
| + | <math>X_{parhuzamos} = \frac{1}{ \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) }</math> | ||
Látható a fentiekből, hogy ha az X<sub>L</sub>-ek összege megegyezik az X<sub>C</sub>-k összegével, akkor soros kapcsolás esetén az eredő reaktancia zérus lesz, párhuzamos kapcsolás esetén a reciprokösszegek egyezősége esetén a reaktancia végtelen értékű lenne. Hamar rájöhetünk, hogy ez utóbbit használjuk ki párhuzamos rezgőkörök esetén. | Látható a fentiekből, hogy ha az X<sub>L</sub>-ek összege megegyezik az X<sub>C</sub>-k összegével, akkor soros kapcsolás esetén az eredő reaktancia zérus lesz, párhuzamos kapcsolás esetén a reciprokösszegek egyezősége esetén a reaktancia végtelen értékű lenne. Hamar rájöhetünk, hogy ez utóbbit használjuk ki párhuzamos rezgőkörök esetén. | ||
| 74. sor: | 88. sor: | ||
Ezen rész megértéséhez a [[komplex számábrázolás]] fogalmának ismerete elengedhetetlen. | Ezen rész megértéséhez a [[komplex számábrázolás]] fogalmának ismerete elengedhetetlen. | ||
| − | '''Soros kapcsolásuk esetén az impedancia:''' <math>Z_{soros} = R_1 + R_2 + ... + R_k + j \Big( X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} ) \Big)</math> | + | '''Soros kapcsolásuk esetén az impedancia:''' <br> |
| + | <math>Z_{soros} = R_1 + R_2 + ... + R_k + j \Big( X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} ) \Big)</math> | ||
| − | '''Párhuzamos kapcsolásuk esetén az impedancia:''' <math>Z_{parhuzamos} = \frac{1}{ \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_k} - j\Big( \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) \Big) }</math> | + | '''Párhuzamos kapcsolásuk esetén az impedancia:''' <br> |
| + | <math>Z_{parhuzamos} = \frac{1}{ \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_k} - j\Big( \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) \Big) }</math> | ||
Az egyenlet kiszámítása során a nevezőben lesz egy valós és egy képzetes érték. A konjugálttal végigszorozva a számlálót és a nevezőt oldható meg a törtszámítás. Lásd: [[Komplex számábrázolás]]. Vagy pedig célszerű áttérni az exponenciális alakra, és azzal elvégezni az osztást. | Az egyenlet kiszámítása során a nevezőben lesz egy valós és egy képzetes érték. A konjugálttal végigszorozva a számlálót és a nevezőt oldható meg a törtszámítás. Lásd: [[Komplex számábrázolás]]. Vagy pedig célszerű áttérni az exponenciális alakra, és azzal elvégezni az osztást. | ||
| 82. sor: | 98. sor: | ||
Az egyenletből szintén látható, hogy amennyiben X<sub>L</sub> megegyezik X<sub>C</sub>-vel, akkor soros kapcsolás esetén az eredő impedancia tisztán ohmos lesz és az ellenállások összege lesz, párhuzamos kapcsolásnál pedig ebben az esetben nem csökkenti az impedanciát a komplex tag, tehát ekkor éri el az impedancia a maximumát, amit az ellenálláshálózat határoz meg. | Az egyenletből szintén látható, hogy amennyiben X<sub>L</sub> megegyezik X<sub>C</sub>-vel, akkor soros kapcsolás esetén az eredő impedancia tisztán ohmos lesz és az ellenállások összege lesz, párhuzamos kapcsolásnál pedig ebben az esetben nem csökkenti az impedanciát a komplex tag, tehát ekkor éri el az impedancia a maximumát, amit az ellenálláshálózat határoz meg. | ||
| − | Azt is meg kell jegyeznünk, hogy mivel u<sub>C</sub> = i*X<sub>C</sub>, megdöbbentően nagy feszültségek lehetnek soros kapcsolás esetén a kondenzátoron. Illetve ugyanez igaz az induktivitásra is. Miközben az egész áramkört tápláló váltakozóáramú generátor feszültsége akár nagyságrendekkel is kisebb. | + | Azt is meg kell jegyeznünk, hogy mivel <br> |
| + | u<sub>C</sub> = i*X<sub>C</sub>, <br> | ||
| + | megdöbbentően nagy feszültségek lehetnek soros kapcsolás esetén a kondenzátoron. Illetve ugyanez igaz az induktivitásra is. Miközben az egész áramkört tápláló váltakozóáramú generátor feszültsége akár nagyságrendekkel is kisebb. | ||
Hogyan lehet ez? A kondenzátoron és az induktivitáson rezonancia esetén pontosan 180 fokos fázistolás van soros kapcsolás esetén a feszültség, párhuzamos kapcsolás esetén az áramaik közt. Ezáltal egymásba juttatják át az energiát és az áramkörön belül végeznek nagy intenzitású oszcillációt. | Hogyan lehet ez? A kondenzátoron és az induktivitáson rezonancia esetén pontosan 180 fokos fázistolás van soros kapcsolás esetén a feszültség, párhuzamos kapcsolás esetén az áramaik közt. Ezáltal egymásba juttatják át az energiát és az áramkörön belül végeznek nagy intenzitású oszcillációt. | ||
| 108. sor: | 126. sor: | ||
== Feszültséggenerátorok soros kapcsolása == | == Feszültséggenerátorok soros kapcsolása == | ||
| − | Egyenfeszültség esetén: <math>U_{0_{soros}} = U_{0_1} + U_{0_2} + \dots + U_{0_n}</math> | + | Egyenfeszültség esetén: <br> |
| + | <math>U_{0_{soros}} = U_{0_1} + U_{0_2} + \dots + U_{0_n}</math> | ||
| − | A belső ellenállás: <math>R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}</math> | + | A belső ellenállás: <br> |
| + | <math>R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}</math> | ||
== Feszültséggenerátorok párhuzamos kapcsolása == | == Feszültséggenerátorok párhuzamos kapcsolása == | ||
| 116. sor: | 136. sor: | ||
<math>U_0 = \frac{G_{b_1} \cdot U_{b_1} + G_{b_2} \cdot U_{b_2} + \dots + G_{b_n} \cdot U_{b_n}}{G_{b_1} + G_{b_2} + \dots + G_{n_b}}</math> | <math>U_0 = \frac{G_{b_1} \cdot U_{b_1} + G_{b_2} \cdot U_{b_2} + \dots + G_{b_n} \cdot U_{b_n}}{G_{b_1} + G_{b_2} + \dots + G_{n_b}}</math> | ||
| − | A belső vezetés: <math>G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}</math> | + | A belső vezetés: <br> |
| + | <math>G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}</math> | ||
== Áramgenerátorok soros kapcsolása == | == Áramgenerátorok soros kapcsolása == | ||
| 122. sor: | 143. sor: | ||
<math>I_0 = \frac{ R_{b_1} \cdot I_{b_1} + R_{b_2} \cdot I_{b_2} + \dots + R_{b_n} \cdot I_{b_n}}{R_{b_1} + R_{b_2} + \dots + R_{n_b}}</math> | <math>I_0 = \frac{ R_{b_1} \cdot I_{b_1} + R_{b_2} \cdot I_{b_2} + \dots + R_{b_n} \cdot I_{b_n}}{R_{b_1} + R_{b_2} + \dots + R_{n_b}}</math> | ||
| − | A belső ellenállás: <math>R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}</math> | + | A belső ellenállás: <br> |
| + | <math>R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}</math> | ||
== Áramgenerátorok párhuzamos kapcsolása == | == Áramgenerátorok párhuzamos kapcsolása == | ||
| 128. sor: | 150. sor: | ||
<math>I_{b_{parhuzamos}} = I_{b_1} + I_{b_2} + \dots + I_{b_n}</math> | <math>I_{b_{parhuzamos}} = I_{b_1} + I_{b_2} + \dots + I_{b_n}</math> | ||
| − | A belső vezetés: <math>G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}</math> | + | A belső vezetés: <br> |
| + | <math>G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}</math> | ||
= Kapcsolók (logikai műveletek) = | = Kapcsolók (logikai műveletek) = | ||
| 138. sor: | 161. sor: | ||
Logikai ''vagy'' műveletnek felel meg. Az áramkörön akkor folyik áram, ha legalább egy kapcsolón folyik. | Logikai ''vagy'' műveletnek felel meg. Az áramkörön akkor folyik áram, ha legalább egy kapcsolón folyik. | ||
| + | |||
| + | = Erősítők, csillapítók soros kapcsolása = | ||
| + | |||
| + | Sorbakapcsolt erősítők és/vagy csillapítók eredő erősítése az egyes erősítések szorzata: <br> | ||
| + | <math>A_{soros} = A_{1} * A_{2} * \dots * A_{n}</math> . | ||
| + | |||
| + | [[Logaritmikus egységek]]kel kifejezve: <br> | ||
| + | <math>A_{soros} = A_{1} + A_{2} + \dots + A_{n}</math> . | ||
[[Kategória:Műszaki alapfogalmak]] | [[Kategória:Műszaki alapfogalmak]] | ||
A lap 2008. november 16., 23:32-kori változata
Tartalomjegyzék
Ellenállások
Ellenállások soros kapcsolása
Soros kapcsolás esetén az eredő ellenállás az egyes ellenállások összege. Azaz
[math]R_{soros} = R_{1} + R_{2} + \dots + R_{n}[/math]
Az ellenálláson eső feszültség soros kapcsolás esetén:
[math]U_{R_{kiszemelt}} = U_{be} \cdot \frac{R_{kiszemelt}}{R_{soros}}[/math], ahol
- Ube a tápfeszültség,
- Rkiszemelt amin akarom tudni,
- Rsoros pedig a fent számított eredő ellenállás.
Érdemes megjegyezni, hogy az így kiszámított elemi feszültségek összege éppen a bemenő feszültséget kell hogy adja.
Az ellenálláson átfolyó áram:
[math]I = \frac{U_{be}}{R_{soros}}[/math]
Soros kapcsolás esetén minden komponens árama ugyanakkora.
Elektromos vezetéssel kifejezve:
[math]G_{soros} = \frac{1}{\frac{1}{G_1} + \frac{1}{G_2} + \dots + \frac{1}{G_n}}[/math]
Ellenállások párhuzamos kapcsolása
Párhuzamos kapcsolás esetén a az eredő vezetés az egyes ellenállások vezetésének összege. Mivel a vezetés az ellenállás reciproka (1/R), ezért
[math]R_{parhuzamos} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}}[/math]
Az ellenállásokon eső feszültség: tekintettel arra, hogy mindegyik ugyanoda van kötve, ezért megegyezik.
Az ellenállásokon átfolyó áram:
[math]I = U_{be} \cdot \frac{\frac{1}{R_{kiszemelt}}}{\frac{1}{R_{parhuzamos}}} = U_{be} \cdot \frac{R_{parhuzamos}}{R_{kiszemelt}}[/math].
Az áramok összege pedig a tápláló áram.
Elektromos vezetéssel kifejezve:
[math]G_{parhuzamos} = G_{1} + G_{2} + \dots + G_{n}[/math]
Kapacitások
Kapacitások soros kapcsolása
[math]C_{soros} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2} + \dots + \frac{1}{C_n}}[/math]
Kapacitások párhuzamos kapcsolása
[math]C_{parhuzamos} = C_{1} + C_{2} + \dots + C_{n}[/math]
Induktivitások
Induktivitások soros kapcsolása
Ha az induktivitások között nincs csatolás:
[math]L_{soros} = L_1 + L_2 + \dots + L_n[/math]
Két, csatolásban lévő induktivitás esetén:
[math]L_{soros} = L_1 + L_2 + 2*M[/math], ahol
- M a kölcsönös induktivitás.
Induktivitások párhuzamos kapcsolása
Ha az induktivitások között nincs csatolás:
[math]L_{parhuzamos} = \frac{1}{\frac{1}{L_1} + \frac{1}{L_2} + \dots + \frac{1}{L_n}}[/math]
Két, csatolásban lévő induktivitás esetén:
[math]L = \frac{L_1 \cdot L_2 - M^2}{L_1 + L_ 2 - M}[/math], ahol
- M a kölcsönös induktivitás.
LC és RLC tagok
Kapacitásokból illetve induktivitásokból álló váltakozóáramú hálózat
A kapacitás reaktanciáját XC, az induktivitásét XL -lel jelöljük.
Soros kapcsolásuk:
[math]X_{soros} = X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} )[/math]
Párhuzamos kapcsolásuk:
[math]X_{parhuzamos} = \frac{1}{ \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) }[/math]
Látható a fentiekből, hogy ha az XL-ek összege megegyezik az XC-k összegével, akkor soros kapcsolás esetén az eredő reaktancia zérus lesz, párhuzamos kapcsolás esetén a reciprokösszegek egyezősége esetén a reaktancia végtelen értékű lenne. Hamar rájöhetünk, hogy ez utóbbit használjuk ki párhuzamos rezgőkörök esetén.
Az elemi komponenseken eső feszultség és áram kiszámítása megegyezik az ellenállásokénál tárgyalttal, azzal a különbséggel, hogy
- R helyett X jelölést alkalmazunk.
- XC és XL feszültség illetve áramiránya egymáshoz viszonyítva ellentétes értékű. A feszültségek összegzésekor erre legyünk tekintettel.
Ellenállásból, kapacitásból és induktivitásból álló váltakozó áramú hálózat
Ezen rész megértéséhez a komplex számábrázolás fogalmának ismerete elengedhetetlen.
Soros kapcsolásuk esetén az impedancia:
[math]Z_{soros} = R_1 + R_2 + ... + R_k + j \Big( X_{L_1} + X_{L_2} + \dots + X_{L_n} - ( X_{C_1} + X_{C_2} + ... + X_{C_m} ) \Big)[/math]
Párhuzamos kapcsolásuk esetén az impedancia:
[math]Z_{parhuzamos} = \frac{1}{ \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_k} - j\Big( \frac{1}{X_{L_1}} + \frac{1}{X_{L_2}} + \dots + \frac{1}{X_{L_n}} - ( \frac{1}{X_{C_1}} + \frac{1}{X_{C_2}} + \dots + \frac{1}{X_{C_m}} ) \Big) }[/math]
Az egyenlet kiszámítása során a nevezőben lesz egy valós és egy képzetes érték. A konjugálttal végigszorozva a számlálót és a nevezőt oldható meg a törtszámítás. Lásd: Komplex számábrázolás. Vagy pedig célszerű áttérni az exponenciális alakra, és azzal elvégezni az osztást.
Az egyenletből szintén látható, hogy amennyiben XL megegyezik XC-vel, akkor soros kapcsolás esetén az eredő impedancia tisztán ohmos lesz és az ellenállások összege lesz, párhuzamos kapcsolásnál pedig ebben az esetben nem csökkenti az impedanciát a komplex tag, tehát ekkor éri el az impedancia a maximumát, amit az ellenálláshálózat határoz meg.
Azt is meg kell jegyeznünk, hogy mivel
uC = i*XC,
megdöbbentően nagy feszültségek lehetnek soros kapcsolás esetén a kondenzátoron. Illetve ugyanez igaz az induktivitásra is. Miközben az egész áramkört tápláló váltakozóáramú generátor feszültsége akár nagyságrendekkel is kisebb.
Hogyan lehet ez? A kondenzátoron és az induktivitáson rezonancia esetén pontosan 180 fokos fázistolás van soros kapcsolás esetén a feszültség, párhuzamos kapcsolás esetén az áramaik közt. Ezáltal egymásba juttatják át az energiát és az áramkörön belül végeznek nagy intenzitású oszcillációt.
Diódák, tranzisztorok
Diódák soros kapcsolása
Ha egy darab egyenirányító dióda záróirányú feszültségtűrése kevés, akkor több, azonos típusú diódát kötnek sorba. Gyártási szórás miatt azonban a záróirányú ellenállás különbözik az egyes diódáknál. Így a feszültség nem egyenletesen olszlik el a diódák között. Könnyen lehet olyan dióda, amelyre túlfeszültség jut, amitől tönkremegy, magával rántva a többit. Az egyenletes feszültségeloszlást külső feszültségosztóval lehet elérni. Gyakorlatban ez minden diódával párhuzamosan kötött, azonos, aránylag nagy értékű ( pl. 100 kiloohm ) ellenállásokkal érhető el. Az ellenállásoknak is ki kell bírniuk a diódákra jutó záróirányú feszültséget.
Feszültségstabilizálásra záróirányban bekötött zener diódát és nyitóirányban bekötött diódát vagy LED-et használnak. Az így sorbakötött félvezetők jellemző feszültségei összeadódnak.
Diódák, tranzisztorok párhuzamos kapcsolása
Ha egy darab félvezetőn ( ( egyenirányító, fénykibocsátó ) diódán, tranzisztoron ) átfolyó áram ( fényerő ) kevés, akkor több, azonos típusú félvezetőt kötnek párhuzamosan. Gyártási szórás miatt azonban a nyitóirányú ellenállás különbözik az egyes félvezetőknél. Így az áram nem egyenletesen olszlik el a félvezetők között. Könnyen lehet olyan félvezető, amelyre túláram jut, amitől tönkremegy. Az egyenletes árameloszlást külső aklatrésszel lehet elérni. Gyakorlatban ez minden félvezetővel sorosan kötött, azonos, aránylag kis értékű ( pl. 0.1 ohm ) ellenállással érhető el. Az ellenállásoknak is ki kell bírniuk a diódákra jutó áramerősséget.
Diódák antiparallel kapcsolása
Az antiparallel kapcsolás olyan párhuzamos kapcsolás, amelyben két polarizált alkatrész egymással ellenétesen ( szemben ) van összekapcsolva.
Antiparallel kapcsolt diódák alkalmasak váltóáramú feszültségstabilizálásra, feszültségkorlátozásra. Kétszínű LED-ek a rákapcsolt áram irányától függően különböző színnel világítanak, mindössze két kivezetés illetve vezeték felhasználásával.
Feszültség- és áramgenerátorok
Feszültséggenerátorok soros kapcsolása
Egyenfeszültség esetén:
[math]U_{0_{soros}} = U_{0_1} + U_{0_2} + \dots + U_{0_n}[/math]
A belső ellenállás:
[math]R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}[/math]
Feszültséggenerátorok párhuzamos kapcsolása
[math]U_0 = \frac{G_{b_1} \cdot U_{b_1} + G_{b_2} \cdot U_{b_2} + \dots + G_{b_n} \cdot U_{b_n}}{G_{b_1} + G_{b_2} + \dots + G_{n_b}}[/math]
A belső vezetés:
[math]G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}[/math]
Áramgenerátorok soros kapcsolása
[math]I_0 = \frac{ R_{b_1} \cdot I_{b_1} + R_{b_2} \cdot I_{b_2} + \dots + R_{b_n} \cdot I_{b_n}}{R_{b_1} + R_{b_2} + \dots + R_{n_b}}[/math]
A belső ellenállás:
[math]R_{b_{soros}} = R_{b_1} + R_{b_2} + \dots + R_{b_n}[/math]
Áramgenerátorok párhuzamos kapcsolása
[math]I_{b_{parhuzamos}} = I_{b_1} + I_{b_2} + \dots + I_{b_n}[/math]
A belső vezetés:
[math]G_{b_{parhuzamos}} = G_{b_1} + G_{b_2} + \dots + G_{b_n}[/math]
Kapcsolók (logikai műveletek)
Kapcsolók soros kapcsolása
Logikai és műveletnek felel meg. Az áramkörön akkor folyik áram, ha minden kapcsolón folyik áram.
Kapcsolók párhuzamos kapcsolása
Logikai vagy műveletnek felel meg. Az áramkörön akkor folyik áram, ha legalább egy kapcsolón folyik.
Erősítők, csillapítók soros kapcsolása
Sorbakapcsolt erősítők és/vagy csillapítók eredő erősítése az egyes erősítések szorzata:
[math]A_{soros} = A_{1} * A_{2} * \dots * A_{n}[/math] .
Logaritmikus egységekkel kifejezve:
[math]A_{soros} = A_{1} + A_{2} + \dots + A_{n}[/math] .