„Kvarc” változatai közötti eltérés
a (Kép középre) |
|||
| 7. sor: | 7. sor: | ||
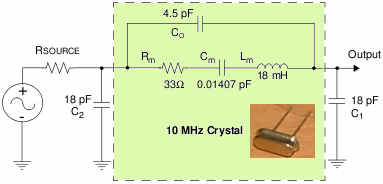
Az egyszerűség kedvéért vegyünk egy 10 MHz-es kvarcot, amely jellemzőin keresztül bemutatásra kerül néhány konkrét érték. | Az egyszerűség kedvéért vegyünk egy 10 MHz-es kvarcot, amely jellemzőin keresztül bemutatásra kerül néhány konkrét érték. | ||
| − | [[Kép:Kvarc helyettesitokepe.gif]] | + | [[Kép:Kvarc helyettesitokepe.gif|center]] |
A fenti ábra egy 10 MHz-es kvarc helyettesítő képét mutatja. Ebből ténylegesen visszaszámolható néhány érdekes paraméter. | A fenti ábra egy 10 MHz-es kvarc helyettesítő képét mutatja. Ebből ténylegesen visszaszámolható néhány érdekes paraméter. | ||
A lap 2008. október 27., 14:14-kori változata
A kvarckristályok igen fontos felhasználási területe a pontos frekvenciájú oszcillátor.
Tartalomjegyzék
Működése
Jellemzői
Az egyszerűség kedvéért vegyünk egy 10 MHz-es kvarcot, amely jellemzőin keresztül bemutatásra kerül néhány konkrét érték.
A fenti ábra egy 10 MHz-es kvarc helyettesítő képét mutatja. Ebből ténylegesen visszaszámolható néhány érdekes paraméter.
Soros rezonanciafrekvencia
[math]f_s = \frac{1}{2\pi\sqrt{L_mC_m}} = \frac{1}{2\pi\sqrt{18\cdot10^{-3}\cdot0.01407\cdot10^{-12}}}=10,00085 MHz[/math]
Párhuzamos rezonanciafrekvencia (csak a kvarc)
[math]f_p = \frac{1}{2\pi\sqrt{L_m \frac{C_m \cdot C_0}{C_m+C_0}}} = \frac{1}{2\pi\sqrt{18\cdot10^{-3}\frac{0.01407\cdot10^{-12}\cdot4.5\cdot10^{-12}}{0.01407\cdot10^{-12} + 4.5\cdot10^{-12}}}} = 10,01647 MHz[/math]
Párhuzamos rezonanciafrekvencia (az ábrán látható kondenzátorokkal körbeépítve)
És hogy a dolog még bonyolultabb legyen: nézzünk rá az ábrára jobban. Látható, hogy a kvarc körbe van építve kettő darab 18 pF-os kondenzátorral, amelyet úgy is felfoghatunk, mintha két soros 18 pF-os kondi lenne párhuzamosan kapcsolva a 4,5 pF-os kondenzátorral. azaz Cpe = 9 + 4,5 = 13,5 pF-ra nőtt ezzel a kvarc párhuzamos kapacitása. Ekkor az eredő párhuzamos frekvencia:
[math]f_{pe} = \frac{1}{2\pi\sqrt{L_m \frac{C_m \cdot C_{pe}}{C_m+C_{pe}}}} = \frac{1}{2\pi\sqrt{18\cdot10^{-3}\frac{0.01407\cdot10^{-12}\cdot13.5\cdot10^{-12}}{0.01407\cdot10^{-12} + 13.5\cdot10^{-12}}}} = 10,00606 MHz[/math]
A fentiekből látható, hogy a párhuzamos rezonancia a kvarc körbeépítésével közelít a soros rezonanciához.
Jósági tényezője
[math]Q = \frac{X_L}{R_m} = \frac{2 \pi f L}{R_m} = \frac{6.283 \cdot 10^7 \cdot 18 \cdot 10^{-3}}{33} = 34272[/math]
Sávszélessége
Soros szűrőként a sávszélessége a -3 dB-es pontok közt:
[math]B = \frac{f_0}{Q} = \frac{10^7}{34272} = 291,8 Hz[/math]
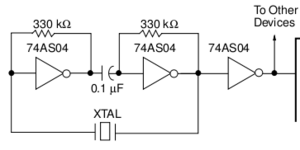
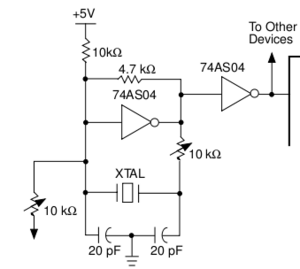
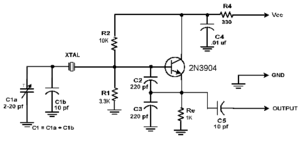
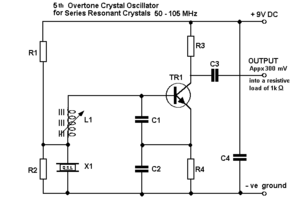
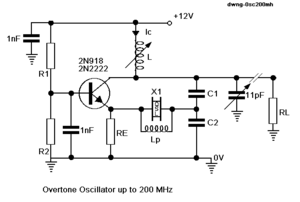
Kvarc alkalmazása oszcillátorokban
Alábbiakban néhány példán keresztül kerül bemutatásra a kvarc oszcillátorokban történő felhasználása. Annyit érdemes tudni a kvarcról, hogy az alapharmonikusa mellett gyengébb amplitudóval jelen van a 3. 5. 7. harmonikus is. Amennyiben az alapharmonikust elnyomjuk, ezek egyikét pedig kiemeljük, akkor a kvarcoszcillátor a kvarcra (mint elektronikai alkatrészre) írt névleges frekvenciaérték 3-szorosán, 5-szörösén vagy 7-szeresén is felhasználható.
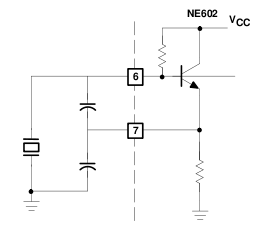
Kvarc alkalmazása szűrőkben
--- megírandó ---