„Impedanciaillesztés” változatai közötti eltérés
a (ábra finomitas - 25 ohm = 2.0-ás SWR) |
a (SWR ábra finomítás) |
||
| 49. sor: | 49. sor: | ||
set output 'allohullamarany-pelda.png' | set output 'allohullamarany-pelda.png' | ||
set grid | set grid | ||
| − | set xtics ( | + | set xtics (8.33,12.5,16.6,25,33.3,50,75,100,150,200,300) |
| − | set size 1.2, 0. | + | set ytics 0.5 |
| − | set yrange [1: | + | set size 1.2, 0.5 |
| − | set xrange [ | + | set yrange [1:6] |
| + | set xrange [8.33:300] | ||
set log x | set log x | ||
set xlabel "Terhelo impedancia" | set xlabel "Terhelo impedancia" | ||
A lap 2006. július 2., 23:39-kori változata
Impedanciaillesztés szerepe a kinyerhető teljesítmény szempontjából
Illesztett kimenetnek nevezzük azt a kimenetet, amely ellenállása megegyezik a terhelés ellenállásával. Ekkor a teljesítmény 50%-a a generátorban fog eldisszipálódni, azonban ekkor jut a legnagyobb teljesítmény a fogyasztóra.
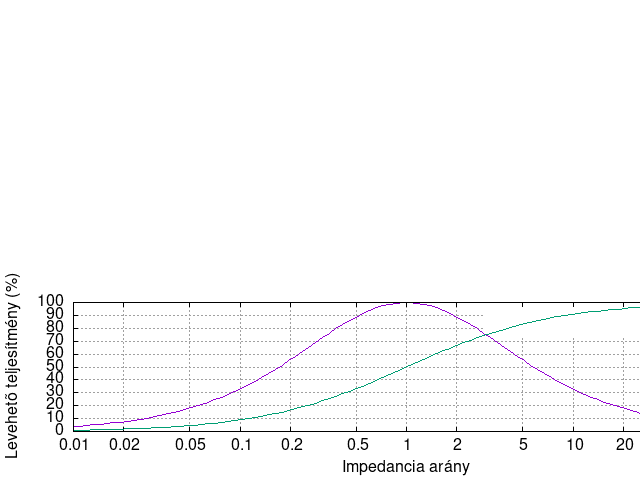
A fenti ábra szerint ha a fogyasztó ellenállása nagyobb, mint a jelforrásé, a hatásfok javul, de a levehető teljesítmény csökken.
Impedanciaillesztés
Egyenáramú körben tehát a terhelés ellenállását és a generátor belső ellenállását azonosra célszerű választani. Ekkor a generátor terheletlen kimenőfeszültségéhez képest fele feszültség jelenik meg a kapcsain, a hatásfok 50% lesz, ellenben ekkor vehető ki belőle a legnagyobb teljesítmény.
Váltakozóáramú körökben a generátor belső impedanciájának konjugáltjára célszerű választani illetve hangolni a terhelés impedanciáját.
Példa:
- Ha a generátorunk 50 ohmos kimenőimpedanciával rendelkezik, akkor 50 ohmos terheléssel vehető ki belőle a legnagyobb teljesítmény.
- Ha a generátorunk 50 ohm + j40 ohm impedanciával rendelkezik, akkor 50 ohm -j40 ohmos komplex impedanciával tudjuk levenni belőle a maximális teljesítményt. Ha egyszerűen csak egy 50 ohmos ellenállást kapcsolunk rá, akkor csak 77%-a lenne kivehető az elméleti maximumnak, miközben a hatásfok is csak 43,8%-os lenne az 50% helyett.
Impedanciaillesztés szerepe a hullámhosszal összemérhető tápvonal esetén
Amennyiben a jelforrás és a fogyasztó közt a jel hullámhosszával összemérhető hosszúságú tápvonal van, akkor az impedanciaillesztés a kivehető maximális teljesítmény mellett egy másik fontos tényező miatt is fontos. Ez a tényező az állóhullám.
A tápvonalak esetén beszélünk haladóhullámról, amelyik a jelforrástól a fogyasztó felé halad, illetve reflektált hullámról, amely a fogyasztótól verődik vissza az illesztetlenség miatt a jelforrás felé.
Az állóhullámarány kiszámítása:
Vezessük be a reflexiós tényező fogalmát, amelyet a fogyasztó felöli kapcson tapasztalható beeső (+) és visszavert (-) feszültségből származtatunk: [math]r=\frac{{U_2}^-}{{U_2}^+}=\frac{Z-Z_0}{Z+Z_0}[/math]
Ebből az állóhullám: [math]\sigma=\frac{1+|r|}{1-|r|}[/math].
Példa: Mekkora lesz a maximális állóhullámom, ha egy 75 ohmos koaxkábelen keresztül egy 50 ohmos fogyasztót hajtok meg? Megoldás: [math]r = \frac{Z-Z_0}{Z+Z_0} = \frac{50-75}{50+75}=-0,2[/math]. Ebből az állóhullámarány: [math]\sigma=\frac{1+|r|}{1-|r|} = \frac{1+|-0.2|}{1-|-0.2|} = \frac{1+0.2}{1-0.2}=\frac{1,2}{0,8} = 1,5[/math].
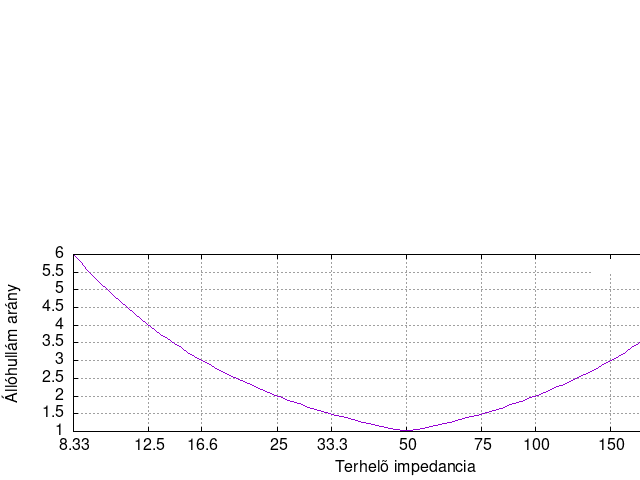
A fenti ábra szemlélteti az állóhullámarány-változást 50 ohmos koaxiális kábelt feltételezve különböző terhelő impedanciák esetén.