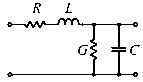„Tápvonalak” változatai közötti eltérés

Innen: HamWiki
Ugrás a navigációhoz Ugrás a kereséshez
a (URL frissítés)
 
(52 közbenső módosítás, amit 7 másik szerkesztő végzett, nincs mutatva)
1. sor: 1. sor:
−
== Elmélet: hullámimpedancia ==
+
= A tápvonal szerepe =
  
−
Koax kábel hullámellenállása: <math>Z_0=\frac{60}{\sqrt{\varepsilon}} ln \frac{b}{a} [\Omega]</math>
+
A '''tápvonalak''' legfontosabb feladata a rádiófrekvenciás jel a forrástól az antenna vagy vevő felé való továbbítása. Ezen kívül még az alábbira használható:
−
vagy aki ln-t nem szereti, 10-es alapú logaritmussal kifejezve: <math>Z_0=\frac{138}{\sqrt{\varepsilon}} * lg \frac{b}{a} [\Omega]</math>
 
  
−
Ahol ''b'' a köpeny átmérő, ''a'' pedig a melegér átmérő. Epszilon a dielektrikum dielektromos állandója.
+
* soros vagy párhuzamos rezgőkörként - ráadásul sokkal jobb [[jósági tényező]]vel rendelkezik, mint a tekercsből és kondenzátorból készített.
 +
* [[induktivitás]]ként vagy [[kondenzátor|kapacitás]]ként felhasználva
 +
* fázistoló áramkörként (kerülővezeték) felhasználva
 +
* impedancia transzformálásra (negyedhullámú szakasz)
 +
* tetszőleges impedanciájú pont áthelyezésére (félhullámú szakasz)
  
−
Nyomtatott áramköri lapon adott hullámellenállású szakaszokat lehet kialakítani. Ha az egyik oldal teli fólia, és szélessége jóval több mint a csik, a nyák vastagság d és a másik oldalon a csík b szélességű, akkor a hullámellenállás kb:
+
= Tápvonalak legfontosabb adatai =
  
−
<math>Z_0=\frac{120\pi}{\sqrt{\varepsilon}} \frac{d}{b}</math>
+
* hullámimpedancia: általában 50, (60,) 75, 300, 450 ohmos tápvonalakkal találkozunk.
 +
* veszteség: [[decibel | dB]]/100 méter
 +
* rövidülési tényező: mennyivel rövidebb az adott frekvenciához tartozó hullámhossz a kábelben. Oka: dielektrikum &epsilon;<sub>r</sub> > 1.
 +
* mechanikai adatok: legkisebb hajlítási sugár, átmérő, tömeg
  
−
Az epszilon üvegszálas folirozott lemeznél kb 2.5, papirbakelitnél 3.5-5
+
= Tápvonal típusok =
  
−
példa: 50 Ohmos csikra van szükség egy SWR mérőben. 2mm vastag folirozott lemezen. akkor <math>b=\frac{(2 * 120 * 3.14)}{(50*1.58)} = 9.41 mm</math>!
+
* '''szimmetrikus tápvonal''' (angolul: ''ladder line'' vagy ''twin-lead'')
 +
* '''koax kábel''' (angolul: ''coaxial cable'')
 +
* '''Goubau vezeték''' (angolul: ''Goubau line'' vagy ''Goubou line'')
 +
* '''csőtápvonal''' - mikrohullámra (angolul: ''waveguide'', azaz hullámvezető)
 +
* '''stripline tápvonal''' - tápvonal nyomtatott áramköri lapon
 +
 
 +
= Tápvonal hullámimpedanciája =
 +
 
 +
[[Fájl:Tapvonal helyettesito kep.gif|frame|right|Ilyen tagok ismétlődő egymás után kapcsolásával modellezhető a tápvonal.]]
 +
 
 +
A tápvonal hullámimpedanciája igen fontos paraméter. Ennek jelentőségét úgy képzelhetjük el, mintha egy gumimedence egyik végében hullámot keltve a medence lenne a tápvonal és a medence túlsó fala a fogyasztó. Megfigyelhetjük, hogy a medence faláról a hullámok visszapattannak. Ha a medence fala ugyanolyan ellenállást tanúsítana, mint a medencében található folyadék hullámtani ellenállása, akkor a medence falának rugózásával a hullámok a túlsó falon végeznének mechanikai munkát, energiájukat leadnák és nem lenne '''reflexió'''.
 +
 
 +
Elektromos szempontból ugyanez a helyzet. A hullám magassága a feszültség, a hullámfront haladása pedig az áramerősség. Ha a tápvonalat a névleges hullámimpedanciájával sikerül lezárni, akkor nem lesz visszaverődő hullám, reflexiómentes lezárásról beszélhetünk.
 +
 
 +
A tápvonal hullámimpedanciája kiszámítható az alábbi összefüggésből:
 +
 
 +
<math>Z_0 = \sqrt{\frac{R + j \omega L}{G + j \omega C}} \approx \sqrt{\frac{L}{C}}</math>
 +
<szamolo sor=4 oszlop=15 jobb>L = 157 nano;C = 61,5 piko;;Z = gyok(L/C)</szamolo>
 +
 
 +
;ahol:
 +
* Z<sub>0</sub> a hullámimpedancia
 +
* R: a két vezető adott hosszán (pl. 1 méter) mérhető soros ellenállása (elhanyagolható)
 +
* L: a két vezető adott hosszán (pl. 1 méter) mérhető induktivitása
 +
* G: a két vezető közt adott hosszban (pl. 1 méter) mérhető vezetés (elhanyagolható)
 +
* C: a két vezető közt adott hosszban (pl. 1 méter) mérhető kapacitás (kis frekvencián kapacitásmérővel kimérhető)
 +
 
 +
;Hullámellenállás mérése: Egy koaxiális kábel hullámellenállását induktivitás és kapacitás mérésével is meghatározhatjuk. Az elhanyagolható veszteségű tápvonalak esetén a soros ellenállás (R) és a szigetelő vezetése (G) elhanyagolható, így két paraméter kimérése szükséges:
 +
* L a végén rövidrezárt kábel induktivitása
 +
* C a végén nyitott kábel kapacitása
 +
 
 +
Egy 630 mm hosszúságú, 5 mm külső átmérőjű, teflon dielektrikumú kábelen a következő eredmények adódtak: C = 61,5 pF és L = 157 nH. Ebből a fenti képlettel számított hullámellenállás Z = 50,6 Ohm, ami az adott kábel gyári adata.
 +
 
 +
== Szimmetrikus tápvonal hullámimpedanciája ==
 +
 
 +
Angol neve: ''ladder line'' vagy ''twin-lead''.
 +
 
 +
[[Fájl:Szalagkabel.jpg|center]]
 +
 
 +
<szamolo sor=5 oszlop=28 jobb>D = 100 milli;d = 1,3 milli;er = 1;;Z = 120/gyok(er)*ln(2*D/d);</szamolo>
 +
 
 +
1 méterre eső kapacitása: <math>C = {\pi \epsilon \over cosh^{-1}({D \over 2a})}</math> [F/m]
 +
 
 +
1 méterre eső soros induktivitása: <math>L = {\mu \over \pi} cosh^{-1}\left({D \over 2a}\right)</math> [H/m]
 +
 
 +
Ebből a hullámimpedancia: <math>Z_0 = \frac{120}{\sqrt{\varepsilon_r}} \cdot ln \Big(\frac{2D}{d}\Big) = \frac{276,4}{\sqrt{\varepsilon_r}} \cdot log_{10} \Big(\frac{2D}{d}\Big) [\Omega]</math>
 +
 
 +
;ahol:
 +
* ''d'': a vezető átmérője,
 +
* ''D'': a vezetők távolsága (D/d nagyobb 2,5 esetén jó a fenti képlet!)
 +
* ''&epsilon;<sub>r</sub>'' (epszilon): a dielektrikum relatív [[dielektromos állandó]]ja (levegő esetén 1).
 +
 
 +
[[Fájl:Szimmetrikus tapvonal.jpg|thumb|Szimmetrikus tápvonal házilag]]
 +
 
 +
;Példa:
 +
 
 +
0.75 mm<sup>2</sup> keresztmetszetű hangszóróvezeték 1 mm átmérőjű. Ebből ha szeretnénk szimmetrikus tápvonalat az alábbi impedanciákkal:
 +
 
 +
* 300 ohmos: 6 mm távolságra kell elhelyezni a két vezetéket (&plusmn;5 %: 5,5 .. 7 mm),
 +
* 450 ohmos: 21,5 mm távolságra kell elhelyezni a két vezetéket (&plusmn;5 %: 17,5 .. 25,5 mm),
 +
* 600 ohmos: 74 mm távolságra kell elhelyezni a két vezetéket (&plusmn;5 %: 58 .. 95 mm)
 +
 
 +
Észrevehető, hogy ha dupla átmérőjű rézvezetőt használunk, akkor a távolságokat is duplázni kell ugyanakkora hullámimpedancia eléréséhez. Az elkészítésének leg egyszerűbb módja, ha a két végén behasított száraz fa vagy inkább műanyag (utóbbi nem nedvesedik át esőben!) távtartóba belenyomott vezetéket beleragasztjuk.
 +
 
 +
== Koaxiális tápvonal (koaxkábel) hullámimpedanciája ==
 +
 
 +
Angol elnevezése: ''coaxial cable''.
 +
 
 +
[[Fájl:Rg-58.jpg|center|frame|RG-58 vékony koaxkábel. Nem igazán jó paraméterű, ámde vékony, hajlékony és könnyű.]]
 +
[[Fájl:Legszigetelt tapvonal keresztmetszete.jpg|thumb|Légszigetelt vastag koaxiális tápvonal, GHz-eken is kis veszteságű, továbbá a mérete miatt nagy teljesítmény szállítására is alkalmas.]]
 +
 
 +
1 méterre eső kapacitása: <math>C = {2 \pi \epsilon \over \ln(D/d)}= {2 \pi \epsilon_0 \epsilon_r \over \ln(D/d)}</math> [F/m]
 +
 
 +
1 méterre eső soros induktivitása: <math>L = {\mu \over 2 \pi} \ln(D/d)= {\mu_0 \mu_r \over 2 \pi} \ln(D/d)</math> [H/m]
 +
 
 +
<szamolo sor=5 oszlop=25 jobb>D = 3 milli;d = 0.8 milli;er = 2,5;;Z = 60/gyok(er)*ln(D/d);</szamolo>
 +
 
 +
Ebből a hullámimpedancia: <math>Z_0 = \frac{1}{2\pi}\sqrt{\frac{\mu}{\varepsilon}} ln \frac{D}{d} = \frac{60}{\sqrt{\varepsilon_r}} ln \frac{D}{d} = \frac{138}{\sqrt{\varepsilon_r}} log_{10} \frac{D}{d} [\Omega]</math>
 +
 
 +
;ahol:
 +
* ''D'': az árnyékolás belső átmérője,
 +
* ''d'': a melegér átmérője,
 +
* ''&epsilon;<sub>r</sub>'' (epszilon): a dielektrikum relatív [[dielektromos állandó]]ja (levegő esetén 1).
 +
 
 +
;Példa: 10-es belméretű alucsőben ritkán elhelyezett távtartókkal 4 mm átmérőjű pálcát vezetünk végig. Ekkor kiszámítható, hogy 55 ohm lesz a hullámimpedanciája.
 +
 
 +
== Goubau vezeték ==
 +
 
 +
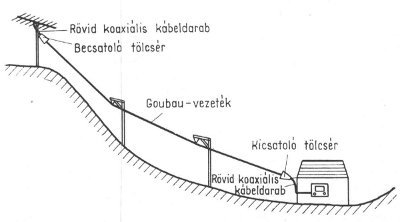
[[Fájl:Goubau vezetek.jpg|frame|left|Goubau vezeték felhasználása nagyobb távolságú kis veszteségű tápvonalként.]]
 +
 
 +
Egy igen érdekes, egyvezetékes jelvezeték, amely főként UHF-en és mikrohullámon jöhet számításba. Angol elnevezése: ''Goubau line'' vagy ''Goubou line''. Felépítését tekintve egy vastagabb központi vezetőből és egy azt körülvevő vastag, nagy relatív dielektromos állandóval rendelkező szigetelőből áll. Az energia többi részét pedig a levegő szállítja.
 +
 
 +
Az energia 90 %-a a vezetőt körülvevő 0,7 &lambda; sugarú körben terjed, a maradék 10 % pedig ezen kívül, nagyjából 2 .. 3 &lambda; sugarú körben.
 +
 
 +
Tehát az energia a vezető és az azt körülvevő szabad térben terjed. A vezető és az azt körülvevő nagy &epsilon;<sub>r</sub>-rel rendelkező szigetelő szerepe tulajdonképp az elektromágneses hullám irányban tartása és a kanyarokkal is tarkított árviteli úton a fogyasztóhoz (pl. antenna!) irányítása.
 +
 
 +
A tölcsér ajánlott hossza 1 &lambda;, ajánlott átmérője 0,5 &lambda;. A koaxkábel meleg ere a Goubau vezeték, az árnyékolása pedig a tölcsérre van kötve.
 +
 
 +
A Goubau vezeték előnye: igen kis csillapítású (koaxkábelhez képest csak 1/10...1/20-ad része!), nagyon jó paraméterű tápvonal készíthető általa.
 +
 
 +
Hátránya: tölcséres meghajtás a generátor és a fogyasztó felöli oldalon egyaránt, továbbá az éles íveket, 20 foknál nagyobb irányváltoztatásokat kerülni kell, mert ilyen helyeken a sugárzás jelentős része elhagyhatja a vezető által kijelölt irányt. Jegesedés a csillapítását erőteljesen növeli.
 +
 
 +
;Megjegyzés: a működése az alábbiakban, a csőtápvonalaknál ismertetett TM mód szerint történik. A vezető körül kialakuló mágneses tér merőleges a hullámterjedés irányra. Közben a vezető körül hosszanti irányban alakulnak ki elektromos erővonalak. A ''Dr. Istvánffy Edvin Tápvonalak, antennák, hullámterjedés'' című könyvének 220. oldala alapján egy 2,5 mm átmérőjű vörösréz huzal 0,35 mm vastag polietilén bevonattal 1,7 GHz-en 2,3 dB/100 méter csillapítást mutatott, 2,4 GHz-en 3,15 dB/100 métert (vessd össze: H-500 koax 1,7 GHz-en 20 dB/100 méter, 2 GHz-en 22 dB/100 méter). 250 MHz-en nem volt észlelhető az eső és jegesedés hatása, 2 GHz-en azonban már 12 dB/100 méter csillapításnövekedést szenvedtek.
 +
 
 +
== Csőtápvonal ==
 +
 
 +
A '''csőtápvonal''' a [[mikrohullám]]on (> 5GHz) használatos, ahol a hullámhossz összemérhetővé válik a tápvonal átmérőjével.
 +
 
 +
[[Kép:Waveguide.jpg]]
 +
[[Kép:Waveguide2.jpg]]
 +
 
 +
Jellemzője, hogy a koaxiális kábellel ellentétben nincs középső vezetője, ezt a rezonáns üreg pótolja. A hullám a csőtápvonalban levegőben és nem műanyag [[dielektrikum]]ban terjed, ezért a csőtápvonal csillapítása kisebb, mint a koax kábelé.
 +
 
 +
Összességében háromféle hullámterjedési módot különböztetünk meg, amelyből kettő vonatkozik a csőtápvonalakra:
 +
 
 +
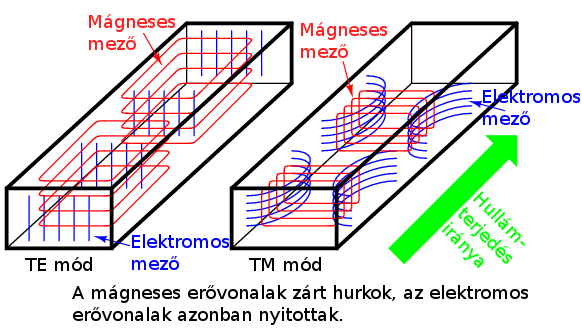
[[Fájl:Csotapvonal_te_tm.png|frame|right|TE<sub>10</sub> és TM<sub>10</sub> mód szemléltetése. Ez akkor keletkezik, ha a csőtápvonal szélessége fél és egész hullámhossz között van. Ha meghaladja a félhullámhossz többszörösét, akkor az ábrán láthatótól eltérő kinézetű, magasabb indexű TE és TM módok jönnek létre.]]
 +
 
 +
;TEM mód: keresztirányú elektromos és mágneses (transverse elektric and magnetic), amelyről akkor beszélhetünk, ha legalább kettő vezető viszi az információt és mind a mágneses tere mind az elektromos tere merőleges a hullám haladási irányára. Azaz kábeleknél, és nem csőtápvonal esetén.
 +
 
 +
;TE mód: keresztirányú elektromos (transverse electric), amely esetben a hullámimpedancia:
 +
 
 +
:<math>Z = \frac{Z_{0}}{\sqrt{1 - \left( \frac{f_{h}}{f}\right)^{2}}} = \frac{Z_{0}}{\sqrt{1 - \left( \frac{\lambda}{2 \cdot szelesseg}\right)^{2}}}</math>
 +
 
 +
;TM mód: keresztirányú mágneses (transverse magnetic), amely esetében a hullámimpedancia:
 +
 
 +
:<math>Z = Z_{0} \sqrt{1 - \left( \frac{f_{h}}{f}\right)^{2}} = Z_{0} \sqrt{1 - \left( \frac{\lambda}{2 \cdot szelesseg}\right)^{2}}</math>
 +
 
 +
<szamolo sor=5 oszlop=55 jobb>Z0 = 377;szelesseg = 68,6 milli;hullhossz = 130 milli;Zte = Z0 / gyok(1 - negyzet(hullhossz/(2*szelesseg)));Ztm = Z0 * gyok(1 - negyzet(hullhossz/(2*szelesseg)));</szamolo>
 +
 
 +
ahol:
 +
* Z<sub>0</sub> a közeg hullámimpedanciája. Levegő esetén <math>Z_0 = \sqrt{\mu \over \varepsilon} = \sqrt{{4 \pi \cdot 10^{-7} H/m} \over {8,854 \cdot 10^{-12} F/m}} = 377 \Omega (\approx 120 \pi \Omega)</math>
 +
* f<sub>h</sub> a határfrekvencia, amely az a frekvencia, ahol a tápvonal szélesebbik oldala félhullámhossz méretű. Csak ennél a frekvenciánál nagyobb frekvenciájú jelet képes vezetni a tápvonal. Ebből mellékesen következik, hogy a jelenséget kihasználva felüláteresztő szűrő is készíthető.
 +
 
 +
== Stripline tápvonal és hullámimpedanciája ==
 +
 
 +
Stripline tápvonal nyomtatott áramköri lapon kialakított, adott hullámellenállású szakasz. Angol elnevezése: ''stripline''. Továbbá egy másik variáns a ''microstrip'' illetve ha például leszívókört szeretnénk, akkor a ''spurline''.
 +
 
 +
Ha a lap egyik oldal teli fólia, és szélessége jóval nagyobb mint a felső oldalon levő csíké, a nyák vastagság ''d'' és a másik oldalon a csík ''b'' szélességű, akkor a hullámellenállás körülbelül:
 +
 
 +
<math>Z_0 = \frac{120\pi}{\sqrt{\varepsilon}} \cdot \frac{d}{b} = \frac{377}{\sqrt{\varepsilon}} \cdot \frac{d}{b}</math>
 +
<szamolo sor=5 oszlop=45 jobb>NYÁKvastagság = 2 milli;csíkszélesség = 4 milli;er=2,5;;Z = 377/gyok(er)*NYÁKvastagság/csíkszélesség</szamolo>
 +
 
 +
Az &epsilon; üvegszálas folirozott lemeznél kb 2.5, papirbakelitnél 3.5 .. 5 közötti.
 +
 
 +
;Példa:
 +
 
 +
50 Ohmos csikra van szükség egy SWR mérőben. 2 mm vastag folirozott lemezen. akkor <math>b=\frac{377}{\sqrt{2,5}} \cdot \frac{2 mm}{50 ohm} = 9,54 mm</math> széles.
  
 
A nemszimmetrikus lapos tápvonalak pontosan nehezen méretezhetők a hat féle Descartes összetevő miatt, de gyakorlatban elég pontos a fenti képlet.
 
A nemszimmetrikus lapos tápvonalak pontosan nehezen méretezhetők a hat féle Descartes összetevő miatt, de gyakorlatban elég pontos a fenti képlet.
  
−
== Koaxkábelek adatai ==
+
= Tápvonal vesztesége (csillapítása) =
 +
 
 +
Belátható, hogy a soros induktív [[reaktancia]] és a párhuzamos kapacitív reaktancia és a terhelés feszültségosztót képez. Annál nagyobb feszültség megy ki a tápvonal túloldalán,
 +
 
 +
* minél kisebb a soros induktivitás.
 +
* minél kisebb a párhuzamos kapacitás.
 +
 
 +
A kapacitás csökkenthető, ha &epsilon;<sub>r</sub> értékét a levegő 1-es értéke felé csökkentjük. Azaz
 +
 
 +
* habosítják, megszaggatják a dielektrikumot illetve kisebb &epsilon;<sub>r</sub> értékkel rendelkező szigetelővel gyárják.
 +
* netán el is hagyják és csak 120 fokonként elhelyezett távtartóval tartják helyén a meleg eret, szalagkábel esetén is csak időnként tesznek távtartót. Egyébként levegő a dielektrikum.
  
 +
Gyakorlatban mérhető értékek:
 +
<szamolo sor=8 oszlop=30 jobb szoveg="Hány dB-t csillapít X méter kábel adott frekvencián?">f_kat = 100 mega;a_kat = 15;;f = 434 mega;hossz = 10;;a_100m = a_kat*gyok(f/f_kat);A_hossz= a_100m*hossz/100</szamolo>
 
{| border="1"
 
{| border="1"
−
! Neve !! <math>Z_0 [\Omega]</math> !! Rövidülés
+
! Név !! Átmérő !! Veszteség @ 100 MHz
 +
|-
 +
| RG-178 || 2 mm || 30 dB/100 méter
 +
|-
 +
| RG-174 || 2,8 mm || 25 dB/100 méter
 +
|-
 +
| RG-58 || 4,95 mm || 15 dB/100 méter
 +
|-
 +
| RG-213 || 9,5 mm || 7,8 dB/100 méter
 
|-
 
|-
−
| RG 58 || 50 || 0.66
+
| H-155 || 5,4 mm || 9,3 dB/100 méter || habosított
 
|-
 
|-
−
| RG 213 || 50 ||
+
| H-500 || 9,8 mm || 4,8 dB/100 méter || habosított
 
|-
 
|-
−
| H-500 || 50 || 0.81
+
| Aircom plus || 10,3 mm || 3,3 dB/100 méter || teflon?
 
|}
 
|}
 +
 +
A csillapításról még azt kell tudni, hogy a frekvencia arány négyzetgyökével növekszik, illetve a kábel hosszával egyenes arányosságban. Tehát ha arra vagyunk kíváncsiak, hogy 10 méter RG-58 434 MHz-en mennyit csillapít, akkor
 +
 +
* a fenti táblázatból tudjuk, hogy 100 MHz-en 15 dB-t csillapít 100 méter.
 +
* 434 MHz-en 100 méteres szakasz: 15 dB * négyzetgyök(434/100) = 15*2.08 = körülbelül 31 dB-t csillapít.
 +
* A fenti paraméterekkel 100 méter helyett 10 méteres szakasz 10/100 * 31 dB = körülbelül 3,1 dB-t fog csillapítani a 10 méteres szakasz.
 +
 +
Ha a csillapítást logaritmusos mértékegységben méred, akkor
 +
 +
<math> A = a_{kat} \cdot \sqrt{\dfrac{f}{f_{kat}}} \cdot l\,</math>
 +
 +
* A = teljesítmény csillapítás, [A] = dB
 +
* a<sub>kat</sub> = fajlagos csillapítás katalógusadata f<sub>kat</sub> frekvencián, [a<sub>kat</sub>] = dB/m
 +
* f = frekvencia, [f] = Hz
 +
* f<sub>kat</sub> = fajlagos csillapításhoz tartozó frekvencia, [f] = Hz
 +
* l = kábelhossz, [l] = m
 +
 +
Ha a csillapítást ''nem logaritmusos'' mértékegységben méred, akkor
 +
 +
<math> A = a_{kat}^{\sqrt{\dfrac{f}{f_{kat}}} \cdot l}\,</math>
 +
 +
* A = teljesítmény csillapítás, [A] = 1
 +
* a<sub>kat</sub> = fajlagos csillapítás katalógusadata f<sub>kat</sub> frekvencián, [a<sub>kat</sub>] = 1<sup>(1/m)</sup>
 +
 +
Csillapítást [https://hg9ieg.hu/szamolo/_sz/APU_aflPU.html számoló].
 +
 +
;A kábelveszteség meghatározása méréssel:
 +
 +
* Zárjuk le a kábelt impedanciájának megfelelő műterheléssel. Ezt 50 MHz-ig akár felületszerelt ellenállások felhasználásával is megoldhatjuk. 2 méteren és 70 centiméteren a műterhelés már odafigyelést igényel, mert a szórt kapacitás már jelentős nem megfelelő szerelésnél.
 +
* Hajtsuk meg a kábelt 1-2 watt teljesítménnyel (akár adóval)
 +
* [[schottky dióda]] segítségével egyenirányítva a jelet, a kábel mindkét végén megmérve és a shottky dióda kisáramú nyitófeszültségét kimérve és hozzáadva már ki is számolhatjuk, hogy mekkora teljesítmény ment a kábelbe és mekkora teljesítmény jutott a műterhelésig. Ebből pedig hogy hány [[decibel]] volt ezen a frekvencián a kábel vesztesége.
 +
 +
= Rövidülési tényező =
 +
 +
A koaxkábel soros induktivitása késlelteti az áram felfutását. A párhuzamos kapacitás szintén gátolja a feszültség megjelenését. Általánosságban elmondható, hogy minél nagyobb a kábel adott egységhosszán mérhető kapacitása, annál nagyobb a rövidülési tényezője.
 +
 +
A tömör műanyag dielektrikumú kábeleknek 0,66-os rövidülése van, a habosított műanyaggal készített kábeleknek 0,8 körüli.
 +
 +
A gyakorlatban ez azt jelenti, hogy például a 2 méteres hullámsávban ha szeretnénk egy félhullámú késleltetést csinálni tápvonallal, akkor nem 1 méteres tápvonal kell, hanem 0,66 illetve 0,8 méter hosszú.
 +
 +
= Tápvonal mint fázistoló =
 +
 +
Az előző pontban ismertetett rövidülési tényezőt is figyelembe véve belátható, hogy tápvonallal lehet adott frekvencián előre meghatározott mértékű fázistolt jelet előállítani, majd az így kapott jelet például összegezni vagy kivonni egymásból.
 +
 +
Egy másik fontos alkalmazása lehet például amikor I és Q keverést szeretnénk végezni, akkor az oszcillátor jelét &lambda;/4 elektromos hosszúságú tápvonallal 90 fokkal késleltethetjük.
 +
 +
= Tápvonal mint reaktáns tag =
 +
 +
A tápvonal hosszának növelésével
 +
 +
* növekszik a (párhuzamos) kapacitása
 +
* növekszik a soros induktivitása
 +
 +
Tudjuk, hogy a kapacitív [[reaktancia]] X<sub>C</sub> = 1 / (2 &pi; f C), az induktív reaktancia pedig X<sub>L</sub> = 2 &pi; f L. Azt is tudjuk, hogy ezek ellentétes fázisban vannak, kivonódnak egymásból.
 +
 +
Mivel a kábel hosszának növeléséve növekszik az induktivitás, ezáltal az X<sub>L</sub> is, továbbá a hossz növelésével növekszik a kapacitás, azaz X<sub>C</sub> fordított arányosságban osztódik, belátható, hogy lesz olyan kábelhossz, ahol X = X<sub>L</sub> - X<sub>C</sub> éppen nulla lesz. Ez éppen a rövidülési tényezővel szorzott negyedhullámú csonk.
 +
 +
Ekkor szakadással lezárt végű kábel esetében kialakul egy soros rezgőkör, a kábelvégen feszültségmaximumot fogunk mérni, a kábel pedig a fenti részben ismertetett hullámimpedancia képletben szereplő R és G tagoktól függő veszteségi ellenállását fogja mutatni.
 +
 +
<szamolo sor=11 oszlop=41 jobb>Z_0 = 50;rövidülés = 0,66;freki = 145 mega;hossz = 1,5;;lambda=rövidülés*c0/freki;XL_rövidzárt=Z_0*tan(360*hossz/lambda);L_rövidzárt =XL_rövidzárt/(2*pi*freki);;Xc_nyitott=Z_0*ctg(360*hossz/lambda);C_nyitott =1/(2*pi*freki*Xc_nyitott);</szamolo>
 +
 +
;Reaktancia a tápvonal hosszának függvényében:
 +
 +
{| border="1"
 +
! Hossz !! Szakadással zárt !! Rövidrezárt végű
 +
|-
 +
| L < &lambda;/4 || kapacitás || induktivitás
 +
|-
 +
| '''L = &lambda;/4''' || '''soros rezgőkör''' || '''párhuzamos rezgőkör'''
 +
|-
 +
| &lambda;/4 < L < &lambda;/2 || induktivitás || kapacitás
 +
|-
 +
| L = &lambda;/2 || párhuzamos rezgőkör || soros rezgőkör
 +
|-
 +
| &lambda;/2 < L < 3*&lambda;/4 || colspan=2 | lásd L < &lambda;/4 (félhullámonként ismétlődik)
 +
|}
 +
 +
További érdekesség, hogy a &lambda;/4-nél hosszabb rövidrezárt végű tápvonal reaktanciája tangens függvény szerint alakul, azaz X<sub>L</sub> = Z<sub>0</sub> * tan(2&pi;*L/&lambda;), egy &lambda;/4-nél hosszabb nyitott végű tápvonal kapacitív reaktanciája cotangens függvény szerint fog alakulni, azaz X<sub>C</sub> = Z<sub>0</sub> * ctg(2&pi;*L/&lambda;).
 +
 +
;A negyed hullámhossz meghatározása méréssel:
 +
 +
* vegyünk egy kábelt. Egyik végén kössünk rá egy generátort (kis teljesítményre leszabályozott adót), a másik végét pedig hagyjuk szakadásban.
 +
* a betáplálási pontján nagyfrekvenciás műszerrel (akár [[schottky dióda | shottky diódával]] egyenirányítva és [[digitális multiméter]]rel mérve) mérjük a feszültséget, miközben a generátor frekvenciáját változtatjuk.
 +
* az a frekvencia, ahol minimális feszültséget mérünk szakadással lezárt tápvonalon, az s kábel ''n * &lambda;/4'' hossza, ahol n páratlan érték (1, 3, 5, ...)
 +
* ha ugyanezt a mérést rövidrezárt végű kábellel ismételjük meg, akkor n páros értékénél (2, 4, 6, ...) fog jelentkezni ez a feszültségminimum.
 +
* Ebből kiszámolható a kábel rövidülési tényezője, amely általában 0,66 és 1 közé esik.
 +
 +
= Tápvonal mint impedancia transzformátor =
 +
 +
A Z terheléssel lezárt Z<sub>0</sub> impedanciájú tápvonal bemenő impedanciája az alábbi összefüggéssel számítható ki:
 +
 +
<math>Z_{be} = Z_0 \cdot \frac{Z + jZ_0 \cdot tg(\beta l)}{Z_0 + jZ \cdot tg(\beta l)}</math>
 +
 +
;ahol:
 +
* Z<sub>0</sub>: tápvonal impedanciája
 +
* Z: terhelés impedanciája
 +
* &beta; = 2&pi;/&lambda;, így a &beta;l = 2&pi;*l/&lambda; - azaz a távolság által meghatározott fázistolás (radiánban). Azaz félhullámú tápvonaldarab &beta;l = &pi; (180°), a negyedhullámú tápvonal esetén &beta;l = &pi;/2 (90°).
 +
 +
'''A fenti összefüggést végigszámolva az alábbiakban ismertetett, gyakorlatban jól felhasználható trükkökhöz jutunk.''' A &lambda;/4 hosszú tápvonalnak ''(és páratlan számú többszöröseinek)'' impedancia transzformáló hatása:
 +
 +
<math>Z_{ki} = \frac{Z_0^2}{Z_{be}}</math>
 +
 +
<szamolo sor=4 oszlop=28 jobb>Z_be = 50; Z_ki = 75;;Z_illesztő=gyok(Z_be*Z_ki)</szamolo>
 +
Azaz ha két különböző impedanciájú tápvonalat szeretnénk illeszteni &lambda;/4 hosszú tápvonal segítségével, akkor a közbenső tápvonal impedanciáját
 +
 +
<math>Z_{illeszto \lambda/4} = \sqrt{Z_{be} \cdot Z_{ki}}</math>
 +
 +
Így például ha 50 ohmos koaxkábelt és 75 ohmos koaxkábelt szeretnénk közösíteni, akkor a képletbe behelyettesítve kijön a 61,2 ohm, azaz az 50 ohmos és 75 ohmos koaxkábelt egy közéjük illesztett &lambda;/4 hosszú 60 ohmos koaxkábellel reflexiómentesen összetoldhatjuk.
 +
 +
;&lambda;/4  tápvonal mint impedancia invertáló elem:
 +
 +
* ha rövidrezárjuk a &lambda;/4 végét, akkor a bemenet felöl szakadást mutat,
 +
* ha pedig szakadással zárjuk a végét, akkor kis impedanciát mutat
 +
* ha pedig hullámimpedanciájával zárjuk a végét, akkor a bemeneten is hullámimpedanciáját mutatja
 +
 +
;Félhullámú tápvonal mint impedancia tükröző elem:
 +
 +
A fentiekkel szemben a félhullámú tápvonal úgy is felfogható, mint kettő negyedhullámú egymással szembe kötött tápvonal. Érdekes tulajdonsága, hogy a kábel belsejében alakulnak ki a feszültségmaximumok, a félhullámú kábel két végén ugyanaz az impedancia látszik.
 +
 +
Azaz a félhullámú kábel végére kötött terhelés impedanciáját látjuk a kábel bemenetén is. Azonban ne feledjük, hogy az eltérő impedanciájú terhelés esetén a félhullámú kábel belsejében lezajló lengések
 +
 +
* szállítási veszteséget okoznak
 +
* feszülségmaximum és árammaximum okán a végpontokon mérhető feszültségeknél és áramoknál nagyobb áramot és feszültséget kell a kábelnek elviselnie.
 +
 +
= További transzformálási trükkök =
 +
 +
A negyedhullámú tápvonal impedancia tükröző hatása az előző fejezetben ismertetésre került. Itt további trükkök lesznek ismertetve.
 +
 +
;Fél vagy harmad impedanciájú koaxkábelre van szükségem az illesztéshez: ekkor kettő vagy három vagy akárhány negyedhullámú koaxkábel árnyékolását összekötjük a végeiken és a belső ereket is. Így az eredő impedanciája N-ed része az elemi kábelnek.
 +
 +
;Aszimmetrikus-szimmetrikus illesztés:
 +
 +
# ha azonos az impedancia, szokás köpenyáramot csökkenteni azáltal, hogy néhány menetet feltekernek a koaxból a bekötéshez közel. Ezáltal az aszimmetrikus áramokat induktivitás gátolja, végeredményként leválasztódik a szimmetrikus rész a tápvonal többi részétől.
 +
# szimmetrizálás + impedancia negyedelése: &lambda;/2 hosszú kerülővezetékkel
 +
#* a szimmetrikus forrás mindkét végére a &lambda;/2 hosszú kerülővezeték melegeret kötjük
 +
#* az elvezető aszimmetrikus kábel melegerét a szimmetrikus forrás egyik erére körjük
 +
#* az elvezető aszimmetrikus kábel árnyékolását a kerülővezeték ''mindkét végének'' árnyékolásával egybeforrasztjuk.
 +
 +
[[Kategória:Technikai háttérismeretek]]

A lap jelenlegi, 2021. május 24., 21:42-kori változata

A tápvonal szerepe

A tápvonalak legfontosabb feladata a rádiófrekvenciás jel a forrástól az antenna vagy vevő felé való továbbítása. Ezen kívül még az alábbira használható:

  • soros vagy párhuzamos rezgőkörként - ráadásul sokkal jobb jósági tényezővel rendelkezik, mint a tekercsből és kondenzátorból készített.
  • induktivitásként vagy kapacitásként felhasználva
  • fázistoló áramkörként (kerülővezeték) felhasználva
  • impedancia transzformálásra (negyedhullámú szakasz)
  • tetszőleges impedanciájú pont áthelyezésére (félhullámú szakasz)

Tápvonalak legfontosabb adatai

  • hullámimpedancia: általában 50, (60,) 75, 300, 450 ohmos tápvonalakkal találkozunk.
  • veszteség: dB/100 méter
  • rövidülési tényező: mennyivel rövidebb az adott frekvenciához tartozó hullámhossz a kábelben. Oka: dielektrikum εr > 1.
  • mechanikai adatok: legkisebb hajlítási sugár, átmérő, tömeg

Tápvonal típusok

  • szimmetrikus tápvonal (angolul: ladder line vagy twin-lead)
  • koax kábel (angolul: coaxial cable)
  • Goubau vezeték (angolul: Goubau line vagy Goubou line)
  • csőtápvonal - mikrohullámra (angolul: waveguide, azaz hullámvezető)
  • stripline tápvonal - tápvonal nyomtatott áramköri lapon

Tápvonal hullámimpedanciája

Ilyen tagok ismétlődő egymás után kapcsolásával modellezhető a tápvonal.

A tápvonal hullámimpedanciája igen fontos paraméter. Ennek jelentőségét úgy képzelhetjük el, mintha egy gumimedence egyik végében hullámot keltve a medence lenne a tápvonal és a medence túlsó fala a fogyasztó. Megfigyelhetjük, hogy a medence faláról a hullámok visszapattannak. Ha a medence fala ugyanolyan ellenállást tanúsítana, mint a medencében található folyadék hullámtani ellenállása, akkor a medence falának rugózásával a hullámok a túlsó falon végeznének mechanikai munkát, energiájukat leadnák és nem lenne reflexió.

Elektromos szempontból ugyanez a helyzet. A hullám magassága a feszültség, a hullámfront haladása pedig az áramerősség. Ha a tápvonalat a névleges hullámimpedanciájával sikerül lezárni, akkor nem lesz visszaverődő hullám, reflexiómentes lezárásról beszélhetünk.

A tápvonal hullámimpedanciája kiszámítható az alábbi összefüggésből:

[math]Z_0 = \sqrt{\frac{R + j \omega L}{G + j \omega C}} \approx \sqrt{\frac{L}{C}}[/math] <szamolo sor=4 oszlop=15 jobb>L = 157 nano;C = 61,5 piko;;Z = gyok(L/C)</szamolo>

ahol
  • Z0 a hullámimpedancia
  • R: a két vezető adott hosszán (pl. 1 méter) mérhető soros ellenállása (elhanyagolható)
  • L: a két vezető adott hosszán (pl. 1 méter) mérhető induktivitása
  • G: a két vezető közt adott hosszban (pl. 1 méter) mérhető vezetés (elhanyagolható)
  • C: a két vezető közt adott hosszban (pl. 1 méter) mérhető kapacitás (kis frekvencián kapacitásmérővel kimérhető)
Hullámellenállás mérése
Egy koaxiális kábel hullámellenállását induktivitás és kapacitás mérésével is meghatározhatjuk. Az elhanyagolható veszteségű tápvonalak esetén a soros ellenállás (R) és a szigetelő vezetése (G) elhanyagolható, így két paraméter kimérése szükséges:
  • L a végén rövidrezárt kábel induktivitása
  • C a végén nyitott kábel kapacitása

Egy 630 mm hosszúságú, 5 mm külső átmérőjű, teflon dielektrikumú kábelen a következő eredmények adódtak: C = 61,5 pF és L = 157 nH. Ebből a fenti képlettel számított hullámellenállás Z = 50,6 Ohm, ami az adott kábel gyári adata.

Szimmetrikus tápvonal hullámimpedanciája

Angol neve: ladder line vagy twin-lead.

Szalagkabel.jpg

<szamolo sor=5 oszlop=28 jobb>D = 100 milli;d = 1,3 milli;er = 1;;Z = 120/gyok(er)*ln(2*D/d);</szamolo>

1 méterre eső kapacitása: [math]C = {\pi \epsilon \over cosh^{-1}({D \over 2a})}[/math] [F/m]

1 méterre eső soros induktivitása: [math]L = {\mu \over \pi} cosh^{-1}\left({D \over 2a}\right)[/math] [H/m]

Ebből a hullámimpedancia: [math]Z_0 = \frac{120}{\sqrt{\varepsilon_r}} \cdot ln \Big(\frac{2D}{d}\Big) = \frac{276,4}{\sqrt{\varepsilon_r}} \cdot log_{10} \Big(\frac{2D}{d}\Big) [\Omega][/math]

ahol
  • d: a vezető átmérője,
  • D: a vezetők távolsága (D/d nagyobb 2,5 esetén jó a fenti képlet!)
  • εr (epszilon): a dielektrikum relatív dielektromos állandója (levegő esetén 1).
Szimmetrikus tápvonal házilag
Példa

0.75 mm2 keresztmetszetű hangszóróvezeték 1 mm átmérőjű. Ebből ha szeretnénk szimmetrikus tápvonalat az alábbi impedanciákkal:

  • 300 ohmos: 6 mm távolságra kell elhelyezni a két vezetéket (±5 %: 5,5 .. 7 mm),
  • 450 ohmos: 21,5 mm távolságra kell elhelyezni a két vezetéket (±5 %: 17,5 .. 25,5 mm),
  • 600 ohmos: 74 mm távolságra kell elhelyezni a két vezetéket (±5 %: 58 .. 95 mm)

Észrevehető, hogy ha dupla átmérőjű rézvezetőt használunk, akkor a távolságokat is duplázni kell ugyanakkora hullámimpedancia eléréséhez. Az elkészítésének leg egyszerűbb módja, ha a két végén behasított száraz fa vagy inkább műanyag (utóbbi nem nedvesedik át esőben!) távtartóba belenyomott vezetéket beleragasztjuk.

Koaxiális tápvonal (koaxkábel) hullámimpedanciája

Angol elnevezése: coaxial cable.

RG-58 vékony koaxkábel. Nem igazán jó paraméterű, ámde vékony, hajlékony és könnyű.
Légszigetelt vastag koaxiális tápvonal, GHz-eken is kis veszteságű, továbbá a mérete miatt nagy teljesítmény szállítására is alkalmas.

1 méterre eső kapacitása: [math]C = {2 \pi \epsilon \over \ln(D/d)}= {2 \pi \epsilon_0 \epsilon_r \over \ln(D/d)}[/math] [F/m]

1 méterre eső soros induktivitása: [math]L = {\mu \over 2 \pi} \ln(D/d)= {\mu_0 \mu_r \over 2 \pi} \ln(D/d)[/math] [H/m]

<szamolo sor=5 oszlop=25 jobb>D = 3 milli;d = 0.8 milli;er = 2,5;;Z = 60/gyok(er)*ln(D/d);</szamolo>

Ebből a hullámimpedancia: [math]Z_0 = \frac{1}{2\pi}\sqrt{\frac{\mu}{\varepsilon}} ln \frac{D}{d} = \frac{60}{\sqrt{\varepsilon_r}} ln \frac{D}{d} = \frac{138}{\sqrt{\varepsilon_r}} log_{10} \frac{D}{d} [\Omega][/math]

ahol
  • D: az árnyékolás belső átmérője,
  • d: a melegér átmérője,
  • εr (epszilon): a dielektrikum relatív dielektromos állandója (levegő esetén 1).
Példa
10-es belméretű alucsőben ritkán elhelyezett távtartókkal 4 mm átmérőjű pálcát vezetünk végig. Ekkor kiszámítható, hogy 55 ohm lesz a hullámimpedanciája.

Goubau vezeték

Goubau vezeték felhasználása nagyobb távolságú kis veszteségű tápvonalként.

Egy igen érdekes, egyvezetékes jelvezeték, amely főként UHF-en és mikrohullámon jöhet számításba. Angol elnevezése: Goubau line vagy Goubou line. Felépítését tekintve egy vastagabb központi vezetőből és egy azt körülvevő vastag, nagy relatív dielektromos állandóval rendelkező szigetelőből áll. Az energia többi részét pedig a levegő szállítja.

Az energia 90 %-a a vezetőt körülvevő 0,7 λ sugarú körben terjed, a maradék 10 % pedig ezen kívül, nagyjából 2 .. 3 λ sugarú körben.

Tehát az energia a vezető és az azt körülvevő szabad térben terjed. A vezető és az azt körülvevő nagy εr-rel rendelkező szigetelő szerepe tulajdonképp az elektromágneses hullám irányban tartása és a kanyarokkal is tarkított árviteli úton a fogyasztóhoz (pl. antenna!) irányítása.

A tölcsér ajánlott hossza 1 λ, ajánlott átmérője 0,5 λ. A koaxkábel meleg ere a Goubau vezeték, az árnyékolása pedig a tölcsérre van kötve.

A Goubau vezeték előnye: igen kis csillapítású (koaxkábelhez képest csak 1/10...1/20-ad része!), nagyon jó paraméterű tápvonal készíthető általa.

Hátránya: tölcséres meghajtás a generátor és a fogyasztó felöli oldalon egyaránt, továbbá az éles íveket, 20 foknál nagyobb irányváltoztatásokat kerülni kell, mert ilyen helyeken a sugárzás jelentős része elhagyhatja a vezető által kijelölt irányt. Jegesedés a csillapítását erőteljesen növeli.

Megjegyzés
a működése az alábbiakban, a csőtápvonalaknál ismertetett TM mód szerint történik. A vezető körül kialakuló mágneses tér merőleges a hullámterjedés irányra. Közben a vezető körül hosszanti irányban alakulnak ki elektromos erővonalak. A Dr. Istvánffy Edvin Tápvonalak, antennák, hullámterjedés című könyvének 220. oldala alapján egy 2,5 mm átmérőjű vörösréz huzal 0,35 mm vastag polietilén bevonattal 1,7 GHz-en 2,3 dB/100 méter csillapítást mutatott, 2,4 GHz-en 3,15 dB/100 métert (vessd össze: H-500 koax 1,7 GHz-en 20 dB/100 méter, 2 GHz-en 22 dB/100 méter). 250 MHz-en nem volt észlelhető az eső és jegesedés hatása, 2 GHz-en azonban már 12 dB/100 méter csillapításnövekedést szenvedtek.

Csőtápvonal

A csőtápvonal a mikrohullámon (> 5GHz) használatos, ahol a hullámhossz összemérhetővé válik a tápvonal átmérőjével.

Waveguide.jpg Waveguide2.jpg

Jellemzője, hogy a koaxiális kábellel ellentétben nincs középső vezetője, ezt a rezonáns üreg pótolja. A hullám a csőtápvonalban levegőben és nem műanyag dielektrikumban terjed, ezért a csőtápvonal csillapítása kisebb, mint a koax kábelé.

Összességében háromféle hullámterjedési módot különböztetünk meg, amelyből kettő vonatkozik a csőtápvonalakra:

TE10 és TM10 mód szemléltetése. Ez akkor keletkezik, ha a csőtápvonal szélessége fél és egész hullámhossz között van. Ha meghaladja a félhullámhossz többszörösét, akkor az ábrán láthatótól eltérő kinézetű, magasabb indexű TE és TM módok jönnek létre.
TEM mód
keresztirányú elektromos és mágneses (transverse elektric and magnetic), amelyről akkor beszélhetünk, ha legalább kettő vezető viszi az információt és mind a mágneses tere mind az elektromos tere merőleges a hullám haladási irányára. Azaz kábeleknél, és nem csőtápvonal esetén.
TE mód
keresztirányú elektromos (transverse electric), amely esetben a hullámimpedancia:
[math]Z = \frac{Z_{0}}{\sqrt{1 - \left( \frac{f_{h}}{f}\right)^{2}}} = \frac{Z_{0}}{\sqrt{1 - \left( \frac{\lambda}{2 \cdot szelesseg}\right)^{2}}}[/math]
TM mód
keresztirányú mágneses (transverse magnetic), amely esetében a hullámimpedancia:
[math]Z = Z_{0} \sqrt{1 - \left( \frac{f_{h}}{f}\right)^{2}} = Z_{0} \sqrt{1 - \left( \frac{\lambda}{2 \cdot szelesseg}\right)^{2}}[/math]

<szamolo sor=5 oszlop=55 jobb>Z0 = 377;szelesseg = 68,6 milli;hullhossz = 130 milli;Zte = Z0 / gyok(1 - negyzet(hullhossz/(2*szelesseg)));Ztm = Z0 * gyok(1 - negyzet(hullhossz/(2*szelesseg)));</szamolo>

ahol:

  • Z0 a közeg hullámimpedanciája. Levegő esetén [math]Z_0 = \sqrt{\mu \over \varepsilon} = \sqrt{{4 \pi \cdot 10^{-7} H/m} \over {8,854 \cdot 10^{-12} F/m}} = 377 \Omega (\approx 120 \pi \Omega)[/math]
  • fh a határfrekvencia, amely az a frekvencia, ahol a tápvonal szélesebbik oldala félhullámhossz méretű. Csak ennél a frekvenciánál nagyobb frekvenciájú jelet képes vezetni a tápvonal. Ebből mellékesen következik, hogy a jelenséget kihasználva felüláteresztő szűrő is készíthető.

Stripline tápvonal és hullámimpedanciája

Stripline tápvonal nyomtatott áramköri lapon kialakított, adott hullámellenállású szakasz. Angol elnevezése: stripline. Továbbá egy másik variáns a microstrip illetve ha például leszívókört szeretnénk, akkor a spurline.

Ha a lap egyik oldal teli fólia, és szélessége jóval nagyobb mint a felső oldalon levő csíké, a nyák vastagság d és a másik oldalon a csík b szélességű, akkor a hullámellenállás körülbelül:

[math]Z_0 = \frac{120\pi}{\sqrt{\varepsilon}} \cdot \frac{d}{b} = \frac{377}{\sqrt{\varepsilon}} \cdot \frac{d}{b}[/math] <szamolo sor=5 oszlop=45 jobb>NYÁKvastagság = 2 milli;csíkszélesség = 4 milli;er=2,5;;Z = 377/gyok(er)*NYÁKvastagság/csíkszélesség</szamolo>

Az ε üvegszálas folirozott lemeznél kb 2.5, papirbakelitnél 3.5 .. 5 közötti.

Példa

50 Ohmos csikra van szükség egy SWR mérőben. 2 mm vastag folirozott lemezen. akkor [math]b=\frac{377}{\sqrt{2,5}} \cdot \frac{2 mm}{50 ohm} = 9,54 mm[/math] széles.

A nemszimmetrikus lapos tápvonalak pontosan nehezen méretezhetők a hat féle Descartes összetevő miatt, de gyakorlatban elég pontos a fenti képlet.

Tápvonal vesztesége (csillapítása)

Belátható, hogy a soros induktív reaktancia és a párhuzamos kapacitív reaktancia és a terhelés feszültségosztót képez. Annál nagyobb feszültség megy ki a tápvonal túloldalán,

  • minél kisebb a soros induktivitás.
  • minél kisebb a párhuzamos kapacitás.

A kapacitás csökkenthető, ha εr értékét a levegő 1-es értéke felé csökkentjük. Azaz

  • habosítják, megszaggatják a dielektrikumot illetve kisebb εr értékkel rendelkező szigetelővel gyárják.
  • netán el is hagyják és csak 120 fokonként elhelyezett távtartóval tartják helyén a meleg eret, szalagkábel esetén is csak időnként tesznek távtartót. Egyébként levegő a dielektrikum.

Gyakorlatban mérhető értékek: <szamolo sor=8 oszlop=30 jobb szoveg="Hány dB-t csillapít X méter kábel adott frekvencián?">f_kat = 100 mega;a_kat = 15;;f = 434 mega;hossz = 10;;a_100m = a_kat*gyok(f/f_kat);A_hossz= a_100m*hossz/100</szamolo>

Név Átmérő Veszteség @ 100 MHz
RG-178 2 mm 30 dB/100 méter
RG-174 2,8 mm 25 dB/100 méter
RG-58 4,95 mm 15 dB/100 méter
RG-213 9,5 mm 7,8 dB/100 méter
H-155 5,4 mm 9,3 dB/100 méter habosított
H-500 9,8 mm 4,8 dB/100 méter habosított
Aircom plus 10,3 mm 3,3 dB/100 méter teflon?

A csillapításról még azt kell tudni, hogy a frekvencia arány négyzetgyökével növekszik, illetve a kábel hosszával egyenes arányosságban. Tehát ha arra vagyunk kíváncsiak, hogy 10 méter RG-58 434 MHz-en mennyit csillapít, akkor

  • a fenti táblázatból tudjuk, hogy 100 MHz-en 15 dB-t csillapít 100 méter.
  • 434 MHz-en 100 méteres szakasz: 15 dB * négyzetgyök(434/100) = 15*2.08 = körülbelül 31 dB-t csillapít.
  • A fenti paraméterekkel 100 méter helyett 10 méteres szakasz 10/100 * 31 dB = körülbelül 3,1 dB-t fog csillapítani a 10 méteres szakasz.

Ha a csillapítást logaritmusos mértékegységben méred, akkor

[math] A = a_{kat} \cdot \sqrt{\dfrac{f}{f_{kat}}} \cdot l\,[/math]

  • A = teljesítmény csillapítás, [A] = dB
  • akat = fajlagos csillapítás katalógusadata fkat frekvencián, [akat] = dB/m
  • f = frekvencia, [f] = Hz
  • fkat = fajlagos csillapításhoz tartozó frekvencia, [f] = Hz
  • l = kábelhossz, [l] = m

Ha a csillapítást nem logaritmusos mértékegységben méred, akkor

[math] A = a_{kat}^{\sqrt{\dfrac{f}{f_{kat}}} \cdot l}\,[/math]

  • A = teljesítmény csillapítás, [A] = 1
  • akat = fajlagos csillapítás katalógusadata fkat frekvencián, [akat] = 1(1/m)

Csillapítást számoló.

A kábelveszteség meghatározása méréssel
  • Zárjuk le a kábelt impedanciájának megfelelő műterheléssel. Ezt 50 MHz-ig akár felületszerelt ellenállások felhasználásával is megoldhatjuk. 2 méteren és 70 centiméteren a műterhelés már odafigyelést igényel, mert a szórt kapacitás már jelentős nem megfelelő szerelésnél.
  • Hajtsuk meg a kábelt 1-2 watt teljesítménnyel (akár adóval)
  • schottky dióda segítségével egyenirányítva a jelet, a kábel mindkét végén megmérve és a shottky dióda kisáramú nyitófeszültségét kimérve és hozzáadva már ki is számolhatjuk, hogy mekkora teljesítmény ment a kábelbe és mekkora teljesítmény jutott a műterhelésig. Ebből pedig hogy hány decibel volt ezen a frekvencián a kábel vesztesége.

Rövidülési tényező

A koaxkábel soros induktivitása késlelteti az áram felfutását. A párhuzamos kapacitás szintén gátolja a feszültség megjelenését. Általánosságban elmondható, hogy minél nagyobb a kábel adott egységhosszán mérhető kapacitása, annál nagyobb a rövidülési tényezője.

A tömör műanyag dielektrikumú kábeleknek 0,66-os rövidülése van, a habosított műanyaggal készített kábeleknek 0,8 körüli.

A gyakorlatban ez azt jelenti, hogy például a 2 méteres hullámsávban ha szeretnénk egy félhullámú késleltetést csinálni tápvonallal, akkor nem 1 méteres tápvonal kell, hanem 0,66 illetve 0,8 méter hosszú.

Tápvonal mint fázistoló

Az előző pontban ismertetett rövidülési tényezőt is figyelembe véve belátható, hogy tápvonallal lehet adott frekvencián előre meghatározott mértékű fázistolt jelet előállítani, majd az így kapott jelet például összegezni vagy kivonni egymásból.

Egy másik fontos alkalmazása lehet például amikor I és Q keverést szeretnénk végezni, akkor az oszcillátor jelét λ/4 elektromos hosszúságú tápvonallal 90 fokkal késleltethetjük.

Tápvonal mint reaktáns tag

A tápvonal hosszának növelésével

  • növekszik a (párhuzamos) kapacitása
  • növekszik a soros induktivitása

Tudjuk, hogy a kapacitív reaktancia XC = 1 / (2 π f C), az induktív reaktancia pedig XL = 2 π f L. Azt is tudjuk, hogy ezek ellentétes fázisban vannak, kivonódnak egymásból.

Mivel a kábel hosszának növeléséve növekszik az induktivitás, ezáltal az XL is, továbbá a hossz növelésével növekszik a kapacitás, azaz XC fordított arányosságban osztódik, belátható, hogy lesz olyan kábelhossz, ahol X = XL - XC éppen nulla lesz. Ez éppen a rövidülési tényezővel szorzott negyedhullámú csonk.

Ekkor szakadással lezárt végű kábel esetében kialakul egy soros rezgőkör, a kábelvégen feszültségmaximumot fogunk mérni, a kábel pedig a fenti részben ismertetett hullámimpedancia képletben szereplő R és G tagoktól függő veszteségi ellenállását fogja mutatni.

<szamolo sor=11 oszlop=41 jobb>Z_0 = 50;rövidülés = 0,66;freki = 145 mega;hossz = 1,5;;lambda=rövidülés*c0/freki;XL_rövidzárt=Z_0*tan(360*hossz/lambda);L_rövidzárt =XL_rövidzárt/(2*pi*freki);;Xc_nyitott=Z_0*ctg(360*hossz/lambda);C_nyitott =1/(2*pi*freki*Xc_nyitott);</szamolo>

Reaktancia a tápvonal hosszának függvényében
Hossz Szakadással zárt Rövidrezárt végű
L < λ/4 kapacitás induktivitás
L = λ/4 soros rezgőkör párhuzamos rezgőkör
λ/4 < L < λ/2 induktivitás kapacitás
L = λ/2 párhuzamos rezgőkör soros rezgőkör
λ/2 < L < 3*λ/4 lásd L < λ/4 (félhullámonként ismétlődik)

További érdekesség, hogy a λ/4-nél hosszabb rövidrezárt végű tápvonal reaktanciája tangens függvény szerint alakul, azaz XL = Z0 * tan(2π*L/λ), egy λ/4-nél hosszabb nyitott végű tápvonal kapacitív reaktanciája cotangens függvény szerint fog alakulni, azaz XC = Z0 * ctg(2π*L/λ).

A negyed hullámhossz meghatározása méréssel
  • vegyünk egy kábelt. Egyik végén kössünk rá egy generátort (kis teljesítményre leszabályozott adót), a másik végét pedig hagyjuk szakadásban.
  • a betáplálási pontján nagyfrekvenciás műszerrel (akár shottky diódával egyenirányítva és digitális multiméterrel mérve) mérjük a feszültséget, miközben a generátor frekvenciáját változtatjuk.
  • az a frekvencia, ahol minimális feszültséget mérünk szakadással lezárt tápvonalon, az s kábel n * λ/4 hossza, ahol n páratlan érték (1, 3, 5, ...)
  • ha ugyanezt a mérést rövidrezárt végű kábellel ismételjük meg, akkor n páros értékénél (2, 4, 6, ...) fog jelentkezni ez a feszültségminimum.
  • Ebből kiszámolható a kábel rövidülési tényezője, amely általában 0,66 és 1 közé esik.

Tápvonal mint impedancia transzformátor

A Z terheléssel lezárt Z0 impedanciájú tápvonal bemenő impedanciája az alábbi összefüggéssel számítható ki:

[math]Z_{be} = Z_0 \cdot \frac{Z + jZ_0 \cdot tg(\beta l)}{Z_0 + jZ \cdot tg(\beta l)}[/math]

ahol
  • Z0: tápvonal impedanciája
  • Z: terhelés impedanciája
  • β = 2π/λ, így a βl = 2π*l/λ - azaz a távolság által meghatározott fázistolás (radiánban). Azaz félhullámú tápvonaldarab βl = π (180°), a negyedhullámú tápvonal esetén βl = π/2 (90°).

A fenti összefüggést végigszámolva az alábbiakban ismertetett, gyakorlatban jól felhasználható trükkökhöz jutunk. A λ/4 hosszú tápvonalnak (és páratlan számú többszöröseinek) impedancia transzformáló hatása:

[math]Z_{ki} = \frac{Z_0^2}{Z_{be}}[/math]

<szamolo sor=4 oszlop=28 jobb>Z_be = 50; Z_ki = 75;;Z_illesztő=gyok(Z_be*Z_ki)</szamolo> Azaz ha két különböző impedanciájú tápvonalat szeretnénk illeszteni λ/4 hosszú tápvonal segítségével, akkor a közbenső tápvonal impedanciáját

[math]Z_{illeszto \lambda/4} = \sqrt{Z_{be} \cdot Z_{ki}}[/math]

Így például ha 50 ohmos koaxkábelt és 75 ohmos koaxkábelt szeretnénk közösíteni, akkor a képletbe behelyettesítve kijön a 61,2 ohm, azaz az 50 ohmos és 75 ohmos koaxkábelt egy közéjük illesztett λ/4 hosszú 60 ohmos koaxkábellel reflexiómentesen összetoldhatjuk.

λ/4 tápvonal mint impedancia invertáló elem
  • ha rövidrezárjuk a λ/4 végét, akkor a bemenet felöl szakadást mutat,
  • ha pedig szakadással zárjuk a végét, akkor kis impedanciát mutat
  • ha pedig hullámimpedanciájával zárjuk a végét, akkor a bemeneten is hullámimpedanciáját mutatja
Félhullámú tápvonal mint impedancia tükröző elem

A fentiekkel szemben a félhullámú tápvonal úgy is felfogható, mint kettő negyedhullámú egymással szembe kötött tápvonal. Érdekes tulajdonsága, hogy a kábel belsejében alakulnak ki a feszültségmaximumok, a félhullámú kábel két végén ugyanaz az impedancia látszik.

Azaz a félhullámú kábel végére kötött terhelés impedanciáját látjuk a kábel bemenetén is. Azonban ne feledjük, hogy az eltérő impedanciájú terhelés esetén a félhullámú kábel belsejében lezajló lengések

  • szállítási veszteséget okoznak
  • feszülségmaximum és árammaximum okán a végpontokon mérhető feszültségeknél és áramoknál nagyobb áramot és feszültséget kell a kábelnek elviselnie.

További transzformálási trükkök

A negyedhullámú tápvonal impedancia tükröző hatása az előző fejezetben ismertetésre került. Itt további trükkök lesznek ismertetve.

Fél vagy harmad impedanciájú koaxkábelre van szükségem az illesztéshez
ekkor kettő vagy három vagy akárhány negyedhullámú koaxkábel árnyékolását összekötjük a végeiken és a belső ereket is. Így az eredő impedanciája N-ed része az elemi kábelnek.
Aszimmetrikus-szimmetrikus illesztés
  1. ha azonos az impedancia, szokás köpenyáramot csökkenteni azáltal, hogy néhány menetet feltekernek a koaxból a bekötéshez közel. Ezáltal az aszimmetrikus áramokat induktivitás gátolja, végeredményként leválasztódik a szimmetrikus rész a tápvonal többi részétől.
  2. szimmetrizálás + impedancia negyedelése: λ/2 hosszú kerülővezetékkel
    • a szimmetrikus forrás mindkét végére a λ/2 hosszú kerülővezeték melegeret kötjük
    • az elvezető aszimmetrikus kábel melegerét a szimmetrikus forrás egyik erére körjük
    • az elvezető aszimmetrikus kábel árnyékolását a kerülővezeték mindkét végének árnyékolásával egybeforrasztjuk.
A lap eredeti címe: „https://wiki.ham.hu/index.php?title=Tápvonalak&oldid=14237”