„Logaritmikus egységek” változatai közötti eltérés
(Elgépelés, ábra javítás) |
|||
| (29 közbenső módosítás, amit 4 másik szerkesztő végzett, nincs mutatva) | |||
| 7. sor: | 7. sor: | ||
== Lineáris és logaritmikus ábrázolás == | == Lineáris és logaritmikus ábrázolás == | ||
| − | A fenti problémára a megoldás a logaritmikus ábrázolás. Ekkor az adott tengelyen a 10-szer akkora érték csak 1 egységnyi elmozdulást jelent, a 100-szoros 2 egységnyit, az | + | A fenti problémára a megoldás a logaritmikus ábrázolás. Ekkor az adott tengelyen a 10-szer akkora érték csak 1 egységnyi elmozdulást jelent, a 100-szoros 2 egységnyit, az 1000-szeres 3 egységnyit, ... |
Alább látható egy jó hangfrekvenciás erősítő átviteli karakterisztikája. Először lineáris grafikonon ábrázolva. | Alább látható egy jó hangfrekvenciás erősítő átviteli karakterisztikája. Először lineáris grafikonon ábrázolva. | ||
| 13. sor: | 13. sor: | ||
<gnuplot> | <gnuplot> | ||
set output 'atviteli_karakterisztika_linearis_pelda.png' | set output 'atviteli_karakterisztika_linearis_pelda.png' | ||
| − | set size 1 | + | set terminal png size 600,200 |
| + | set size 1,1 | ||
| + | set grid x | ||
set yrange [5:25] | set yrange [5:25] | ||
set xlabel "Frekvencia (Hz)" | set xlabel "Frekvencia (Hz)" | ||
| − | set ylabel "Erositesi | + | set ylabel "Erositesi arany" |
| + | set samples 1000 | ||
Xc1(x) = 1/(6.283*x*10e-6) | Xc1(x) = 1/(6.283*x*10e-6) | ||
| 29. sor: | 32. sor: | ||
<gnuplot> | <gnuplot> | ||
set output 'atviteli_karakterisztika_logaritmikus_pelda.png' | set output 'atviteli_karakterisztika_logaritmikus_pelda.png' | ||
| − | set size 1 | + | set terminal png size 600,200 |
| + | set size 1,1 | ||
| + | set grid | ||
| + | set xtics (2,5,10,20,50,100,200,500,1000,2000,5000,10000,20000,50000) | ||
set yrange [5:25] | set yrange [5:25] | ||
set xlabel "Frekvencia (Hz)" | set xlabel "Frekvencia (Hz)" | ||
| 39. sor: | 45. sor: | ||
</gnuplot> | </gnuplot> | ||
| − | + | A logaritmikus léptékű ábrához még annyit érdemes megjegyezni, hogy a [[dekád]]on belül az 1/3 és 2/3 távolságban rendre a 2,15 és 4,64 érték található. Gyakorlatban ha egy szélessávú eszköz átviteli karakterisztikát kézzel ábrázoljuk, akkor a dekádot (pl. 1 és 10 közt) kettő vonallal három egyenlő részre osztjuk és a két vonal rendre a 2 és 5 értéket fogja ábrázolni. | |
| − | A logaritmikus | + | == A logaritmikus skála használata == |
| + | |||
| + | A logaritmikus skálát sok okból szeretjük. Egyrészt nincsenek benne olyan bődületes számok, mint a lineáris tér esetén. Ugyanakkor az arányokat szemléletesebben kifejezi, mivel a logaritmikus térben 200 mW és 800 mW közt ugyanakkora a különbség, mint 20 W és 80 W között. | ||
A logaritmikus térben végzett műveletek és lineáris térben gyakorolt hatásuk: | A logaritmikus térben végzett műveletek és lineáris térben gyakorolt hatásuk: | ||
| 50. sor: | 58. sor: | ||
* Ha a logaritmikus érték előjelét megfordítjuk, akkor lineáris térben 10<sup>X</sup> alakban felírt szám 10<sup>-X</sup> -re változik. | * Ha a logaritmikus érték előjelét megfordítjuk, akkor lineáris térben 10<sup>X</sup> alakban felírt szám 10<sup>-X</sup> -re változik. | ||
| − | Tehát elmondható, hogy a logaritmikus | + | Tehát elmondható, hogy a logaritmikus skála ''közelebb hozza'' a nagy értékeket egymáshoz, az értékeknek nem a nagyságukra, hanem arányukra koncentrál. |
A lineáris térben végzett szorzás és osztás műveletek logaritmikus térben összeadásra illetve kivonásra cserélődnek, a hatványozás és gyökvonás pedig szorzásra illetve osztásra. | A lineáris térben végzett szorzás és osztás műveletek logaritmikus térben összeadásra illetve kivonásra cserélődnek, a hatványozás és gyökvonás pedig szorzásra illetve osztásra. | ||
| + | |||
| + | Ezen alapult a ma már nem használatos számolóeszköz, a [http://hu.wikipedia.org/wiki/Logarl%C3%A9c logarléc]. | ||
== A decibel == | == A decibel == | ||
| + | |||
| + | <szamolo sor=4 oszlop=25 jobb>Pbe = 1 milli;Pki = 5;;AdB = 10*log10(Pki/Pbe)</szamolo> | ||
A logaritmikus tér legismertebb felhasználási területe a '''decibel (dB)''' skála. | A logaritmikus tér legismertebb felhasználási területe a '''decibel (dB)''' skála. | ||
| 70. sor: | 82. sor: | ||
=== Decibel feszültségre === | === Decibel feszültségre === | ||
| + | |||
| + | <szamolo sor=4 oszlop=25 jobb>Ube = 100 milli;Uki = 50 milli;;AdB = 20*log10(Uki/Ube)</szamolo> | ||
Tekintettel arra, hogy <math>P=U*I=U*(U/R)=U^2/R</math>, amiből átrendezéssel <math>U=\sqrt{P*R}</math> képlet jön ki. (U a feszültség, I az áram, R az ellenállás, P a teljesítmény). | Tekintettel arra, hogy <math>P=U*I=U*(U/R)=U^2/R</math>, amiből átrendezéssel <math>U=\sqrt{P*R}</math> képlet jön ki. (U a feszültség, I az áram, R az ellenállás, P a teljesítmény). | ||
| 82. sor: | 96. sor: | ||
{| border="1" | {| border="1" | ||
| + | |- style="background: lightgray" | ||
! dB !! teljesítményarány || feszültségarány | ! dB !! teljesítményarány || feszültségarány | ||
|- | |- | ||
| 92. sor: | 107. sor: | ||
| 10 dB || 10 || <math>\sqrt{10} = 3,16</math> | | 10 dB || 10 || <math>\sqrt{10} = 3,16</math> | ||
|- | |- | ||
| − | | | + | | 20 dB || 100 || 10 |
| − | |- | + | |- style="background: lightgray" |
! colspan=3 | Negatív értékekre | ! colspan=3 | Negatív értékekre | ||
|- | |- | ||
| 102. sor: | 117. sor: | ||
| -10 dB || 0,1 || <math>1/\sqrt{10} = 0,316</math> | | -10 dB || 0,1 || <math>1/\sqrt{10} = 0,316</math> | ||
|- | |- | ||
| − | | - | + | | -20 dB || 1/100 || 1/10 |
|} | |} | ||
| − | Néhány jó ujjgyakorlat a fentiek alapján: | + | |
| + | ;Néhány jó ujjgyakorlat a fentiek alapján: | ||
{| border="1" | {| border="1" | ||
| + | |- style="background: lightgray" | ||
! dB !! teljesítményarány || feszültségarány | ! dB !! teljesítményarány || feszültségarány | ||
|- | |- | ||
| 131. sor: | 148. sor: | ||
A címben szereplő értékek dB-es arányszámmal ellátott mértékegységek. | A címben szereplő értékek dB-es arányszámmal ellátott mértékegységek. | ||
| − | * a dBm alapmértékegysége az a teljesítmény, amely 1 mW-ot jelent 600 ohm-ra viszonyítva. Az Ohm-törvény értelmében <math>U=\sqrt{P | + | * a dBm alapmértékegysége az a teljesítmény, amely 1 mW-ot jelent 600 ohm-ra viszonyítva. Az [[Ohm-törvény]] értelmében <math>U=\sqrt{P\cdot R}=\sqrt{0,001 |
| + | ~{\rm W} \cdot 600~\Omega}=\sqrt{0,6}~{\rm V}=0,7746~{\rm V}</math>. A dBm származéka a dBu, amely terhelőimpedanciától függetlenül a 0,7746 V-ot veszi alapegységnek. Hang jelszinteknél használatos mértékegység. | ||
* a dBµV az 1 mikrovoltra vonatkoztatott dB érték. Rádiófrekvencián ezt a mértékegységet használjuk. Alapértelmezetten 50 ohm-os impedanciára vonatkoztatva. A dBmV pedig az 1 mV-ra vonatkoztatott érték - rádiófrekvencián használatos, nagyobb jelek esetén. 1 dBmV = 60 dBµV. Ugyanígy a dBV-ot is alkalmazhatjuk, ahol az alapérték az 1 V. | * a dBµV az 1 mikrovoltra vonatkoztatott dB érték. Rádiófrekvencián ezt a mértékegységet használjuk. Alapértelmezetten 50 ohm-os impedanciára vonatkoztatva. A dBmV pedig az 1 mV-ra vonatkoztatott érték - rádiófrekvencián használatos, nagyobb jelek esetén. 1 dBmV = 60 dBµV. Ugyanígy a dBV-ot is alkalmazhatjuk, ahol az alapérték az 1 V. | ||
| 166. sor: | 184. sor: | ||
'''Megoldás:''' a csillapítást jelöljük negatív előjellel. Ekkor az eredő erősítés A=-8 dB + 25 dB = 17 dB. A jelszint pedig: U<sup>dB</sup>=17+3=20 dBµV-os lesz. Ezt az értéket a decibelskáláról visszaszámolva 10 µV-ot kapunk. | '''Megoldás:''' a csillapítást jelöljük negatív előjellel. Ekkor az eredő erősítés A=-8 dB + 25 dB = 17 dB. A jelszint pedig: U<sup>dB</sup>=17+3=20 dBµV-os lesz. Ezt az értéket a decibelskáláról visszaszámolva 10 µV-ot kapunk. | ||
| − | '''2. Példa:''' Egy 7 dBW-os rádióvégfokra rákötünk | + | '''2. Példa:''' Egy 7 dBW-os rádióvégfokra rákötünk 4 dB csillapítású kábelt, majd 9 dB nyereségű antennára vezetjük. Mekkora [[ERP]]-vel fog sugározni az antenna? |
'''Megoldás:''' P<sup>dB</sup>=7 dBW-4 dB + 9 dB = 12 dBW. Hogy kézzelfogható legyen, valós értékre is átszámolhatjuk. 12 dBW = 3+3+3+3 dB, tehát 2*2*2*2 = 16 W. Tehát a kérdéses ERP 16 W-ra jött ki. | '''Megoldás:''' P<sup>dB</sup>=7 dBW-4 dB + 9 dB = 12 dBW. Hogy kézzelfogható legyen, valós értékre is átszámolhatjuk. 12 dBW = 3+3+3+3 dB, tehát 2*2*2*2 = 16 W. Tehát a kérdéses ERP 16 W-ra jött ki. | ||
| 173. sor: | 191. sor: | ||
A rádiókon az S mérő jelszinteket mutat. De mekkora jelszintnek felel meg az adott S érték? | A rádiókon az S mérő jelszinteket mutat. De mekkora jelszintnek felel meg az adott S érték? | ||
| + | |||
| + | <szamolo jobb sor=9 oszlop=43>S = 5;plusz_dB = 0;;;U_RH_dBµV = 10+(S-5)*6+plusz_dB;U_RH_volt = 1 mikro*exp10(U_RH_dBµV/20);;U_URH_dBµV = -10+(S-5)*6+plusz_dB;U_URH_volt = 1 mikro*exp10(U_URH_dBµV/20)</szamolo> | ||
{| border=1 style="text-align: center" | {| border=1 style="text-align: center" | ||
| 202. sor: | 222. sor: | ||
|} | |} | ||
| − | + | Alternatív meghatározás <!-- HA5LQ tananyaga --> szerint '''rövidhullámon S9 = 50 μV, URH-n 5 μV''', valamint S(n+1) = 2 * S(n). Eme két definíció értékei között kevesebb, mint egy százalék eltérés van. Továbbá dBm-ben kifejezve '''az S5-ös jelszint = -97 dBm RH-n és -117 dBm URH-n'''. | |
| − | |||
| − | |||
| − | Látható továbbá hogy [[rövidhullám]]on az S5-ös jelszint 3 mikrovoltos | + | A fenti táblázat alapján látható, hogy az S értékek 6 dB-enként vannak felosztva, azaz két S fok között a jelfeszültség kétszeresére nő (ami által a teljesítmény a négyszeresére, ami pedig éppen a 6 dB). Látható továbbá hogy [[rövidhullám]]on az S5-ös jelszint 3 mikrovoltos bemenő jelet jelent. [[URH]]-n a kisebb zajszint miatt érzékenyebb vevők építhetők, így ezt az értéket az S mérő 20 dB-lel lejjebb, 0,3 mikrovoltnál mutatja. |
| − | bemenő jelet jelent. | ||
| − | [[URH]]-n a kisebb zajszint miatt érzékenyebb vevők építhetők, így ezt az értéket az S mérő 20 dB-lel lejjebb, 0,3 mikrovoltnál mutatja. | ||
Ez azt is jelenti, hogy amennyiben 6 dB-lel jobb nyereségű antennával forgalmazunk, az mindössze 1 S értéknyit javít a vételen. Azonban ne felejtsük el, amikor S1-et alig akarja elérni a jel, akkor az a 6 dB igen sokat számít. | Ez azt is jelenti, hogy amennyiben 6 dB-lel jobb nyereségű antennával forgalmazunk, az mindössze 1 S értéknyit javít a vételen. Azonban ne felejtsük el, amikor S1-et alig akarja elérni a jel, akkor az a 6 dB igen sokat számít. | ||
| − | + | Az előző szakasz példáján látszik, hogy 5 W kimenőteljesítmény 7 dBW, amennyiben 6 dB-nyi adóteljesítmény növelést szeretnénk, akkor az 13 dBW, azaz 10*2 = 20 W-tal kell adni. | |
| + | |||
| + | == Rádiófrekvenciás eszközök jelszintjei == | ||
| + | |||
| + | {| border="1" | ||
| + | ! Felhasználás || Vételjellemzés || Jelszint | ||
| + | |- | ||
| + | | rowspan="3" | Rádióamatőr RH || S1 || -14 dBµV (0,2 µV) | ||
| + | |- | ||
| + | | S5 || 10 dBµV (3 µV) | ||
| + | |- | ||
| + | | S9 || 34 dBµV (50 µV) | ||
| + | |- | ||
| + | | rowspan="3" | Rádióamatőr URH || S1 || -34 dBµV (0,02 µV) | ||
| + | |- | ||
| + | | S5 || -10 dBµV (0,3 µV) | ||
| + | |- | ||
| + | | S9 || 14 dBµV (5 µV) | ||
| + | |- | ||
| + | | rowspan="5" | CCIR FM rádió || Igen gyenge hang || 20-26 dBµV (10-20 µV) | ||
| + | |- | ||
| + | | Hullámzó hang || 34-40 dBµV (50-100 µV) | ||
| + | |- | ||
| + | | Stabil mono hang || 40-46 dBµV (100-200 µV) | ||
| + | |- | ||
| + | | Jó minőségű, de monó hang || 46-52 dBµV (200-400 µV) | ||
| + | |- | ||
| + | | Sztereo URH hang || 54 dBµV (500 µV) | ||
| + | |- | ||
| + | | rowspan="5" | Analóg TV || Szinkronjel nyomok || 20-26 dBµV (10-20 µV) | ||
| + | |- | ||
| + | | Szinkronizált zajos kép || 34-40 dBµV (50-100 µV) | ||
| + | |- | ||
| + | | Kontrasztos, stabil de zajos kép || 40-46 dBµV (100-200 µV) | ||
| + | |- | ||
| + | | Zajmentes fekete-fehér<br>vagy zajos színes kép || 46-52 dBµV (200-400 µV) | ||
| + | |- | ||
| + | | Zajmentes színes kép || 54 dBµV (500 µV) | ||
| + | |} | ||
| + | |||
| + | A hangfrekvenciás átjátszókábel esetén pedig a 0 dBm (0,775 V) a referencia feszültség. Eredete a vezetékes távbeszélőtechnikában alkalmazott 600 ohmon disszipálódó 1 mW teljesítményre vezetődik vissza. | ||
| + | |||
| + | == neper == | ||
| + | |||
| + | Neper ( John Napier of Merchiston ) egyrészt nem tízes, hanem természetes alapú logaritmust; másrészt nem teljesítmény-, hanem amplitúdó- ( feszültség ) arányt használt. A mértékegység neve neper, jele Np. | ||
| + | |||
| + | <math> A = \ln \frac{U_2}{U_1}\ [Np] </math> | ||
| + | |||
| + | <math> A = \frac{1}{2} \cdot \ln \frac{P_2}{P_1}\ [Np] </math> | ||
| + | |||
| + | == bit == | ||
== Logaritmikus értékek nem rádiótechnikai alkalmazásai == | == Logaritmikus értékek nem rádiótechnikai alkalmazásai == | ||
| 218. sor: | 284. sor: | ||
* [http://hu.wikipedia.org/wiki/Richter-sk%C3%A1la Richter skála] - földrengések erőssége | * [http://hu.wikipedia.org/wiki/Richter-sk%C3%A1la Richter skála] - földrengések erőssége | ||
* [http://hu.wikipedia.org/wiki/Magnit%C3%BAd%C3%B3 magnitúdó] - csillagok fényessége | * [http://hu.wikipedia.org/wiki/Magnit%C3%BAd%C3%B3 magnitúdó] - csillagok fényessége | ||
| − | * [http://hu.wikipedia.org/wiki/ | + | * [http://hu.wikipedia.org/wiki/PH pH] - a víz 7-es pH értékű, alatta savas, felette lugos. |
== Külső hivatkozások == | == Külső hivatkozások == | ||
*[http://www.analog.com/Analog_Root/static/techSupport/designTools/interactiveTools/dbconvert/dbconvert.html V<sub>peak</sub>, V<sub>RMS</sub>, teljesítmény, dBm, dBu, dBV átszámítás] | *[http://www.analog.com/Analog_Root/static/techSupport/designTools/interactiveTools/dbconvert/dbconvert.html V<sub>peak</sub>, V<sub>RMS</sub>, teljesítmény, dBm, dBu, dBV átszámítás] | ||
| + | |||
| + | |||
| + | [[Kategória:Műszaki alapfogalmak]] | ||
A lap jelenlegi, 2013. október 13., 20:27-kori változata
Az embereknek természetes a lineáris ábrázolás. Ez azt jelenti, hogy ami 10-szer messzebb van, azt 10 egység távolságra rajzolom, ami 100 egység távolságra, azt 100 egység távolságra rajzolom.
Műszaki gyakorlatban azonban ez nem mindig praktikus. Talán a legszemléletesebb érv az értéktartomány tágassága. Elegendő arra gondolni, hogy egyetlen grafikonon szeretnénk ábrázolni egy erősítő esetén például egy olyan görbét, amely vízszintes tengelyére a bemenő amplitúdót szeretnénk ábrázolni 1 mikrovolt és 10 millivolt közt, a függőleges tengelyén pedig a kimenetét 1 millivolt és 10 volt közt.
Látható, hogy az ábrán a kis értékek nem lesznek láthatóak, a nagy értékek pedig felesleges részletességgel láthatóak. Ugyanis 1 mV és 10 mV közt jobban érdekel minket a különbség, mint 980 mV és 990 mV közt.
Tartalomjegyzék
Lineáris és logaritmikus ábrázolás
A fenti problémára a megoldás a logaritmikus ábrázolás. Ekkor az adott tengelyen a 10-szer akkora érték csak 1 egységnyi elmozdulást jelent, a 100-szoros 2 egységnyit, az 1000-szeres 3 egységnyit, ...
Alább látható egy jó hangfrekvenciás erősítő átviteli karakterisztikája. Először lineáris grafikonon ábrázolva.
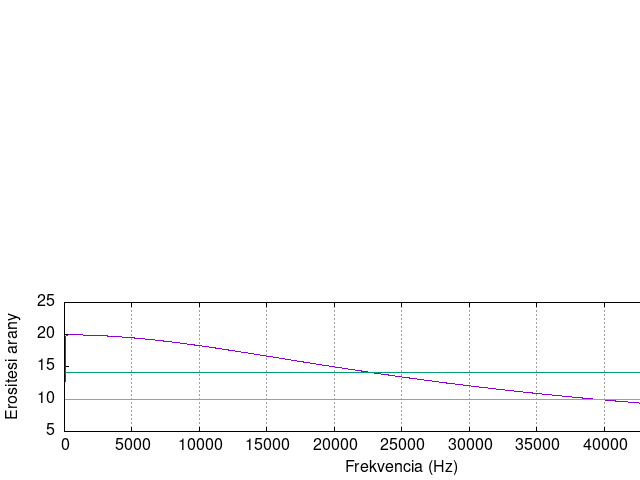
Bár ebből az ábrából pontosan leolvashatjuk (felesleges pontossággal), hogy 20 kHz-nél hol metszi a -3 dB-s vonalat az átviteli karakterisztika, de a 20 Hz-es alsó frekvenciát nem látjuk, illetve a közbenső viselkedése sem szemléletes a fenti erősítőnek.
Amennyiben logaritmikus skálán ábrázoljuk, az ábrából szakavatottak azonnal látják, hogy 20 Hz és 20 kHz közt jó erősítőhöz méltóan viselkedik.
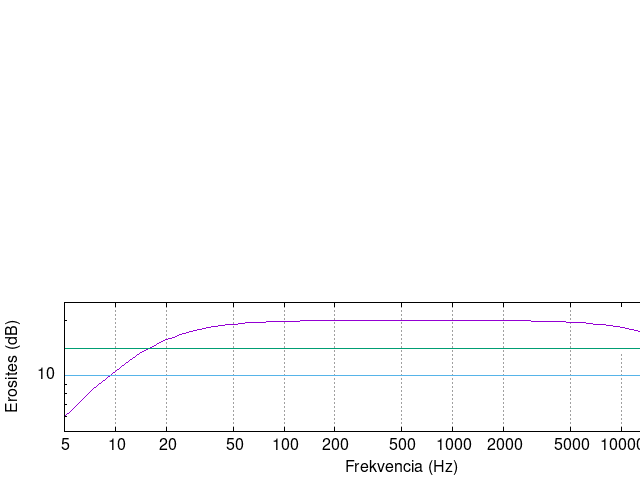
A logaritmikus léptékű ábrához még annyit érdemes megjegyezni, hogy a dekádon belül az 1/3 és 2/3 távolságban rendre a 2,15 és 4,64 érték található. Gyakorlatban ha egy szélessávú eszköz átviteli karakterisztikát kézzel ábrázoljuk, akkor a dekádot (pl. 1 és 10 közt) kettő vonallal három egyenlő részre osztjuk és a két vonal rendre a 2 és 5 értéket fogja ábrázolni.
A logaritmikus skála használata
A logaritmikus skálát sok okból szeretjük. Egyrészt nincsenek benne olyan bődületes számok, mint a lineáris tér esetén. Ugyanakkor az arányokat szemléletesebben kifejezi, mivel a logaritmikus térben 200 mW és 800 mW közt ugyanakkora a különbség, mint 20 W és 80 W között.
A logaritmikus térben végzett műveletek és lineáris térben gyakorolt hatásuk:
- Két logaritmus érték összeadása a lineáris térbeli szorzásnak felel meg.
- Két logaritmikus érték szorzása, lineáris térben hatványozásnak (számX) felel meg.
- Két logaritmikus érték osztása pedig a számlálóban levő szám nevezőedik gyökét adja. Például ha a logaritmikus számot elosztjuk 2-vel, az a lineáris térben a négyzetgyökvonás művelete.
- Ha a logaritmikus érték előjelét megfordítjuk, akkor lineáris térben 10X alakban felírt szám 10-X -re változik.
Tehát elmondható, hogy a logaritmikus skála közelebb hozza a nagy értékeket egymáshoz, az értékeknek nem a nagyságukra, hanem arányukra koncentrál. A lineáris térben végzett szorzás és osztás műveletek logaritmikus térben összeadásra illetve kivonásra cserélődnek, a hatványozás és gyökvonás pedig szorzásra illetve osztásra.
Ezen alapult a ma már nem használatos számolóeszköz, a logarléc.
A decibel
<szamolo sor=4 oszlop=25 jobb>Pbe = 1 milli;Pki = 5;;AdB = 10*log10(Pki/Pbe)</szamolo>
A logaritmikus tér legismertebb felhasználási területe a decibel (dB) skála. Az alapegység a bel (B), csak ez ritkán használatos. A bel-t Alexander Graham Bell amerikai mérnökről és feltalálóról nevezték el. Eredetileg telefonkábelek csillapításának jellemzésére használták, de később a használata más területen is elterjedt.
1 B két (általában teljesítmény jellegű) érték 10-szeres arányát jelenti.
A decibel tehát önmagában pusztán egy arányt jelöl. Például a 3 dB teljesítménynövekedés azt jelenti, hogy valaminek a teljesítménye duplájára nőtt. A -3 dB pedig azt, hogy a teljesítmény a viszonyításhoz képest felére csökkent.
Képlettel: A = 10*log(P2/P1), ahol A a logaritmikus érték, P2 a teljesítmény, amit P1-hez viszonyítunk.
Decibel feszültségre
<szamolo sor=4 oszlop=25 jobb>Ube = 100 milli;Uki = 50 milli;;AdB = 20*log10(Uki/Ube)</szamolo>
Tekintettel arra, hogy [math]P=U*I=U*(U/R)=U^2/R[/math], amiből átrendezéssel [math]U=\sqrt{P*R}[/math] képlet jön ki. (U a feszültség, I az áram, R az ellenállás, P a teljesítmény).
Ez azt jelenti, hogy négyszeres teljesítménynövekedés esetén ugyanazon terhelés kapcsain dupla akkora feszültség jelentkezik, 100-szoros teljesítmény növekedéskor pedig csak 10-szeres feszültség.
Képlettel: A = 20*log(U2/U1), ahol A a logaritmikus érték, U2 a feszültség, amit U1-hez viszonyítunk.
Megjegyzés: ugyanabban az esetben a fenti, teljesítményre vonatkoztatott A arány és a feszültségre vonatkoztatott A értéke ugyanaz az érték.
Néhány dB érték teljesítményre és feszültségre
| dB | teljesítményarány | feszültségarány |
|---|---|---|
| 0 dB | 1 | 1 |
| 3 dB | 2 | [math]\sqrt{2} = 1,414[/math] |
| 6 dB (3+3) | 4 (2*2) | 2 |
| 10 dB | 10 | [math]\sqrt{10} = 3,16[/math] |
| 20 dB | 100 | 10 |
| Negatív értékekre | ||
| -3 dB | 1/2 | [math]1/\sqrt{2} = 0,707[/math] |
| -6 dB (-3 + -3) | 1/4 (1/2*1/2) | 1/2 |
| -10 dB | 0,1 | [math]1/\sqrt{10} = 0,316[/math] |
| -20 dB | 1/100 | 1/10 |
- Néhány jó ujjgyakorlat a fentiek alapján
| dB | teljesítményarány | feszültségarány |
|---|---|---|
| 6 dB = 3+3 | 2*2=4 | 2 |
| 7 dB = 10-3 | 10/2 = 5 | 2,23 (3.16/1,41) |
| 12 dB = 3+3+3+3 | 4*4 = 16 | 4 |
| 13 dB = 10+3 | 10*2 | 4,47 (3,16*1,414) |
| 20 dB = 10+10 | 10*10 = 100 | 10 |
| 30 dB = 20+10 | 100*10 = 1000 | 31,6 |
| 36 dB = 20+10+3+3 | 100*10*2*2 = 4000 | 63,2 |
| -36 dB = -20 + -10 + -3 + -3 | 1/100*1/10*1/2*1/2 = 1/4000 = 0.00025 | 1/63,2 = 0,0158 |
dBm (és dBu), dBµV, dBmV
A címben szereplő értékek dB-es arányszámmal ellátott mértékegységek.
- a dBm alapmértékegysége az a teljesítmény, amely 1 mW-ot jelent 600 ohm-ra viszonyítva. Az Ohm-törvény értelmében [math]U=\sqrt{P\cdot R}=\sqrt{0,001 ~{\rm W} \cdot 600~\Omega}=\sqrt{0,6}~{\rm V}=0,7746~{\rm V}[/math]. A dBm származéka a dBu, amely terhelőimpedanciától függetlenül a 0,7746 V-ot veszi alapegységnek. Hang jelszinteknél használatos mértékegység.
- a dBµV az 1 mikrovoltra vonatkoztatott dB érték. Rádiófrekvencián ezt a mértékegységet használjuk. Alapértelmezetten 50 ohm-os impedanciára vonatkoztatva. A dBmV pedig az 1 mV-ra vonatkoztatott érték - rádiófrekvencián használatos, nagyobb jelek esetén. 1 dBmV = 60 dBµV. Ugyanígy a dBV-ot is alkalmazhatjuk, ahol az alapérték az 1 V.
| Feszültség | dBu | dBV | dBmV | dBµV |
|---|---|---|---|---|
| 1 mV | -57,8 dBu | -60 dBV | 0 dBmV | 60 dBµV |
| 10 mV | -37,8 dBu | -40 dBV | 20 dBmV | 80 dBµV |
| 100 mV | -17,8 dBu | -20 dBV | 40 dBmV | 100 dBµV |
| 1 V | 2,2 dBu | 0 dBV | 60 dBmV | 120 dBµV |
| 10 V | 22,2 dBu | 20 dBV | 80 dBmV | 140 dBµV |
Ahogy létezik dBV (dBmV, dBµV), ugyanúgy használható a dBW (dBmW, dBµW) is. Ez esetben a viszonyítási alap az 1 W (1 mW, 1µW).
Például:
- 5 W a fenti táblázat alapján a 10 W fele, azaz 10-3= 7 dBW.
- 20 W a 10 W duplája, azaz 13 dBW
- 100 W a 10 W 10-szerese, azaz 20 dBW.
- A 0,5 W pedig az 1 W fele, azaz -3 dBW
Gyakorlati felhasználás
1. Példa: Egy 3 dBµV-ot szolgáltató antenna jelét 8 dB veszteségű kábelen hozzuk le, de előtte az antennánál elhelyezünk egy 25 dB-es előerősítőt. Mekkora jelszint lesz a koaxkábel alsó végén?
Megoldás: a csillapítást jelöljük negatív előjellel. Ekkor az eredő erősítés A=-8 dB + 25 dB = 17 dB. A jelszint pedig: UdB=17+3=20 dBµV-os lesz. Ezt az értéket a decibelskáláról visszaszámolva 10 µV-ot kapunk.
2. Példa: Egy 7 dBW-os rádióvégfokra rákötünk 4 dB csillapítású kábelt, majd 9 dB nyereségű antennára vezetjük. Mekkora ERP-vel fog sugározni az antenna?
Megoldás: PdB=7 dBW-4 dB + 9 dB = 12 dBW. Hogy kézzelfogható legyen, valós értékre is átszámolhatjuk. 12 dBW = 3+3+3+3 dB, tehát 2*2*2*2 = 16 W. Tehát a kérdéses ERP 16 W-ra jött ki.
Rádió S értékei
A rádiókon az S mérő jelszinteket mutat. De mekkora jelszintnek felel meg az adott S érték?
<szamolo jobb sor=9 oszlop=43>S = 5;plusz_dB = 0;;;U_RH_dBµV = 10+(S-5)*6+plusz_dB;U_RH_volt = 1 mikro*exp10(U_RH_dBµV/20);;U_URH_dBµV = -10+(S-5)*6+plusz_dB;U_URH_volt = 1 mikro*exp10(U_URH_dBµV/20)</szamolo>
| S érték | Jelszint RH-n | Jelszint URH-n |
|---|---|---|
| S1 | -14 dBµV | -34 dBµV |
| S2 | -8 dBµV | -28 dBµV |
| S3 | -2 dBµV | -22 dBµV |
| S4 | 4 dBµV | -16 dBµV |
| S5 | 10 dBµV | -10 dBµV |
| S6 | 16 dBµV | -4 dBµV |
| S7 | 22 dBµV | 2 dBµV |
| S8 | 28 dBµV | 8 dBµV |
| S9 | 34 dBµV | 14 dBµV |
| S9+20 dB | 54 dBµV | 34 dBµV |
| S9+40 dB | 74 dBµV | 54 dBµV |
| S9+60 dB | 94 dBµV | 74 dBµV |
Alternatív meghatározás szerint rövidhullámon S9 = 50 μV, URH-n 5 μV, valamint S(n+1) = 2 * S(n). Eme két definíció értékei között kevesebb, mint egy százalék eltérés van. Továbbá dBm-ben kifejezve az S5-ös jelszint = -97 dBm RH-n és -117 dBm URH-n.
A fenti táblázat alapján látható, hogy az S értékek 6 dB-enként vannak felosztva, azaz két S fok között a jelfeszültség kétszeresére nő (ami által a teljesítmény a négyszeresére, ami pedig éppen a 6 dB). Látható továbbá hogy rövidhullámon az S5-ös jelszint 3 mikrovoltos bemenő jelet jelent. URH-n a kisebb zajszint miatt érzékenyebb vevők építhetők, így ezt az értéket az S mérő 20 dB-lel lejjebb, 0,3 mikrovoltnál mutatja.
Ez azt is jelenti, hogy amennyiben 6 dB-lel jobb nyereségű antennával forgalmazunk, az mindössze 1 S értéknyit javít a vételen. Azonban ne felejtsük el, amikor S1-et alig akarja elérni a jel, akkor az a 6 dB igen sokat számít.
Az előző szakasz példáján látszik, hogy 5 W kimenőteljesítmény 7 dBW, amennyiben 6 dB-nyi adóteljesítmény növelést szeretnénk, akkor az 13 dBW, azaz 10*2 = 20 W-tal kell adni.
Rádiófrekvenciás eszközök jelszintjei
| Felhasználás | Vételjellemzés | Jelszint |
|---|---|---|
| Rádióamatőr RH | S1 | -14 dBµV (0,2 µV) |
| S5 | 10 dBµV (3 µV) | |
| S9 | 34 dBµV (50 µV) | |
| Rádióamatőr URH | S1 | -34 dBµV (0,02 µV) |
| S5 | -10 dBµV (0,3 µV) | |
| S9 | 14 dBµV (5 µV) | |
| CCIR FM rádió | Igen gyenge hang | 20-26 dBµV (10-20 µV) |
| Hullámzó hang | 34-40 dBµV (50-100 µV) | |
| Stabil mono hang | 40-46 dBµV (100-200 µV) | |
| Jó minőségű, de monó hang | 46-52 dBµV (200-400 µV) | |
| Sztereo URH hang | 54 dBµV (500 µV) | |
| Analóg TV | Szinkronjel nyomok | 20-26 dBµV (10-20 µV) |
| Szinkronizált zajos kép | 34-40 dBµV (50-100 µV) | |
| Kontrasztos, stabil de zajos kép | 40-46 dBµV (100-200 µV) | |
| Zajmentes fekete-fehér vagy zajos színes kép |
46-52 dBµV (200-400 µV) | |
| Zajmentes színes kép | 54 dBµV (500 µV) |
A hangfrekvenciás átjátszókábel esetén pedig a 0 dBm (0,775 V) a referencia feszültség. Eredete a vezetékes távbeszélőtechnikában alkalmazott 600 ohmon disszipálódó 1 mW teljesítményre vezetődik vissza.
neper
Neper ( John Napier of Merchiston ) egyrészt nem tízes, hanem természetes alapú logaritmust; másrészt nem teljesítmény-, hanem amplitúdó- ( feszültség ) arányt használt. A mértékegység neve neper, jele Np.
[math] A = \ln \frac{U_2}{U_1}\ [Np] [/math]
[math] A = \frac{1}{2} \cdot \ln \frac{P_2}{P_1}\ [Np] [/math]
bit
Logaritmikus értékek nem rádiótechnikai alkalmazásai
- Richter skála - földrengések erőssége
- magnitúdó - csillagok fényessége
- pH - a víz 7-es pH értékű, alatta savas, felette lugos.