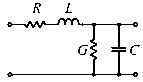Tápvonalak

A tápvonal szerepe

A tápvonalak legfontosabb feladata a rádiófrekvenciás jel a forrástól az antenna vagy vevő felé való továbbítása. Ezen kívül még az alábbira használható:

• soros vagy párhuzamos rezgőkörként - ráadásul sokkal jobb jósági tényezővel rendelkezik, mint a tekercsből és kondenzátorból készített.
• induktivitásként vagy kapacitásként felhasználva
• fázistoló áramkörként (kerülővezeték) felhasználva
• impedancia transzformálásra (negyedhullámú szakasz)
• tetszőleges impedanciájú pont áthelyezésére (félhullámú szakasz)

Tápvonalak legfontosabb adatai

• hullámimpedancia: általában 50, (60,) 75, 300, 450 ohmos tápvonalakkal találkozunk.
• veszteség: dB/100 méter
• rövidülési tényező: mennyivel rövidebb az adott frekvenciához tartozó hullámhossz a kábelben. Oka: dielektrikum ε_r > 1.
• mechanikai adatok: legkisebb hajlítási sugár, átmérő, tömeg

Tápvonal típusok

• szimmetrikus tápvonal
• koax kábel
• csőtápvonal - mikrohullámra
• stripline tápvonal - tápvonal nyomtatott áramköri lapon

Tápvonal hullámimpedanciája

A tápvonal hullámimpedanciája igen fontos paraméter. Ennek jelentőségét úgy képzelhetjük el, mintha egy gumimedence egyik végében hullámot keltve a medence lenne a tápvonal és a medence túlsó fala a fogyasztó. Megfigyelhetjük, hogy a medence faláról a hullámok visszapattannak. Ha a medence fala ugyanolyan ellenállást tanúsítana, mint a medencében található folyadék hullámtani ellenállása, akkor a medence falának rugózásával a hullámok a túlsó falon végeznének mechanikai munkát, energiájukat leadnák és nem lenne reflexió.

Elektromos szempontból ugyanez a helyzet. A hullám magassága a feszültség, a hullámfront haladása pedig az áramerősség. Ha a tápvonalat a névleges hullámimpedanciájával sikerül lezárni, akkor nem lesz visszaverődő hullám, reflexiómentes lezárásról beszélhetünk.

Ilyen tagok ismétlődő egymás után kapcsolásával modellezhető a tápvonal.

A tápvonal hullámimpedanciája kiszámítható az alábbi összefüggésből:

[math]Z_0 = \sqrt{\frac{R + j \omega L}{G + j \omega C}} \approx \sqrt{\frac{L}{C}}[/math]

ahol

• Z₀ a hullámimpedancia
• R: a két vezető adott hosszán (pl. 1 méter) mérhető soros ellenállása (elhanyagolható)
• L: a két vezető adott hosszán (pl. 1 méter) mérhető induktivitása
• G: a két vezető közt adott hosszban (pl. 1 méter) mérhető vezetés (elhanyagolható)
• C: a két vezető közt adott hosszban (pl. 1 méter) mérhető kapacitás (kis frekvencián kapacitásmérővel kimérhető)

Hullámellenállás mérése

Egy koaxiális kábel hullámellenállását induktivitás és kapacitás mérésével is meghatározhatjuk. Az elhanyagolható veszteségű tápvonalak esetén a soros ellenállás (R) és a szigetelő vezetése (G) elhanyagolható, így két paraméter kimérése szükséges:

• L a végén rövidrezárt kábel induktivitása
• C a végén nyitott kábel kapacitása

Egy 630 mm hosszúságú, 5 mm külső átmérőjű, teflon dielektrikumú kábelen a következő eredmények adódtak: C = 61,5 pF és L = 157 nH. Ebből a fenti képlettel számított hullámellenállás Z = 50,6 Ohm, ami az adott kábel gyári adata.

Szimmetrikus tápvonal hullámimpedanciája

1 méterre eső kapacitása: [math]C = {\pi \epsilon \over cosh^{-1}({D \over 2a})}[/math] [F/m]

1 méterre eső soros induktivitása: [math]L = {\mu \over \pi} cosh^{-1}\left({D \over 2a}\right)[/math] [H/m]

Ebből a hullámimpedancia: [math]Z_0 = \frac{120}{\sqrt{\varepsilon_r}} \cdot ln \Big(\frac{2D}{d}\Big) = \frac{276,4}{\sqrt{\varepsilon_r}} \cdot log_{10} \Big(\frac{2D}{d}\Big) [\Omega][/math]

ahol

• d: a vezető átmérője,
• D: a vezetők távolsága (D/d nagyobb 2,5 esetén jó a fenti képlet!)
• ε_r (epszilon): a dielektrikum relatív dielektromos állandója (levegő esetén 1).

Szimmetrikus tápvonal házilag

Példa

0.75 mm² keresztmetszetű hangszóróvezeték 1 mm átmérőjű. Ebből ha szeretnénk szimmetrikus tápvonalat az alábbi impedanciákkal:

• 300 ohmos: 6 mm távolságra kell elhelyezni a két vezetéket (±5 %: 5,5 .. 7 mm),
• 450 ohmos: 21,5 mm távolságra kell elhelyezni a két vezetéket (±5 %: 17,5 .. 25,5 mm),
• 600 ohmos: 74 mm távolságra kell elhelyezni a két vezetéket (±5 %: 58 .. 95 mm)

Észrevehető, hogy ha dupla átmérőjű rézvezetőt használunk, akkor a távolságokat is duplázni kell ugyanakkora hullámimpedancia eléréséhez. Az elkészítésének leg egyszerűbb módja, ha a két végén behasított fa vagy műanyag távtartóba belenyomott vezetéket beleragasztjuk.

Koaxiális tápvonal (koaxkábel) hullámimpedanciája

RG-58 vékony koaxkábel. Nem igazán jó paraméterű, ámde vékony, hajlékony és könnyű.

Légszigetelt vastag koaxiális tápvonal, GHz-eken is kis veszteságű, továbbá a mérete miatt nagy teljesítmény szállítására is alkalmas.

1 méterre eső kapacitása: [math]C = {2 \pi \epsilon \over \ln(D/d)}= {2 \pi \epsilon_0 \epsilon_r \over \ln(D/d)}[/math] [F/m]

1 méterre eső soros induktivitása: [math]L = {\mu \over 2 \pi} \ln(D/d)= {\mu_0 \mu_r \over 2 \pi} \ln(D/d)[/math] [H/m]

Ebből a hullámimpedancia: [math]Z_0 = \frac{1}{2\pi}\sqrt{\frac{\mu}{\varepsilon}} ln \frac{D}{d} = \frac{60}{\sqrt{\varepsilon_r}} ln \frac{D}{d} = \frac{138}{\sqrt{\varepsilon_r}} log_{10} \frac{D}{d} [\Omega][/math]

ahol

• D: az árnyékolás belső átmérője,
• d: a melegér átmérője,
• ε_r (epszilon): a dielektrikum relatív dielektromos állandója (levegő esetén 1).

Példa

10-es belméretű alucsőben ritkán elhelyezett távtartókkal 4 mm átmérőjű pálcát vezetünk végig. Ekkor kiszámítható, hogy 55 ohm lesz a hullámimpedanciája.