„Diszkrét idejű szűrők” változatai közötti eltérés
| 82. sor: | 82. sor: | ||
b: <konvhossz> hosszú együttható vektor a visszacsatoláshoz | b: <konvhossz> hosszú együttható vektor a visszacsatoláshoz | ||
Kimenet: a konvolúció eredménye | Kimenet: a konvolúció eredménye | ||
| − | A kimenetet felejtsük el a főprogramban az eredm vektorhoz hozzáilleszteni, | + | A kimenetet ne felejtsük el a főprogramban az eredm vektorhoz hozzáilleszteni, |
hiszen az alábbi szűrő esetén felhasználjuk a következő számításhoz. | hiszen az alábbi szűrő esetén felhasználjuk a következő számításhoz. | ||
*/ | */ | ||
A lap 2009. február 24., 18:54-kori változata
Tartalomjegyzék
Alapok
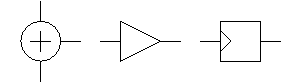
A diszkrét idejű rendszerek 3 alapelem kombinációjából épülnek fel.
- összeadó, amely a két bemenetére érkező értéket előjelesen összegzi. Azaz ki = be1 + be2
- erősítő vagy más néven szorzó, amely egy előre konfigurált konstanssal szorozza a jelet. Azaz ki = konstans * be
- késleltető, amely egyetlen ütemmel (nevezzük órajelnek) késleltetve helyezi a kimenetére (és tartja) a bemeneten levő jelet.
Ebből a hátom alapkomponensből épülnek fel fel a diszkrét idejű hálózatok.
Ezeknek a diszkrét idejű implementációknak számos előnyük van az analóg megoldásokhoz képest. Például:
- pontosság
- egyszerű, olcsó reprodukálhatóság - a szorzók konstansai könnyen reprodukálhatók.
- hőmérsékletfüggetlen működés
- nincs öregedési elhangolódásuk
FIR és IIR szűrő elrendezések
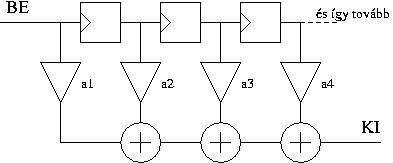
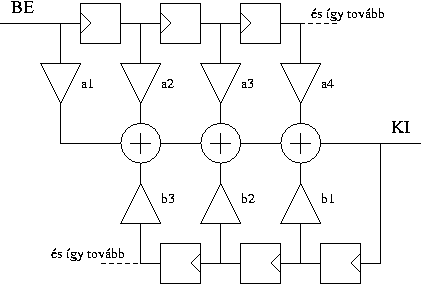
Nézzük meg a különbséget az alábbi ábrákon a FIR és az IIR szűrőelrendezés között. Első ránézésre látszik, hogy az IIR szűrőre a kimenetének késleltetett jele is vissza van vezetve, míg a FIR-nél csak a bemenőjel és annak késleltetésével operálunk.
- FIR (Finite Impulse Response = véges impulzusválaszú), hiszen a késleltető számával történő késleltetés után a bemenetre adott impulzus már tuti nem hat az áramkörre, hiszen ez az impulzus az utolsó késleltetőt (=élvezérelt tárolót) is elhagyta.
- IIR (Infinite Impulse Response = végtelen impulzusválaszú), hiszen a kimenet visszacsatoltja is beleszól a következő kimeneti állapotba.
És még néhány különbség:
| Fázismenet: lineáris fázismenet mindig lehetséges | nehezen kézbentartható, nem léteznek rá pontos módszerek |
| Stabilitás: mindig stabil, oszcillációmentes; tetszőleges mértékben bővíthető | instabillá (gerjedővé) tervezhető, oszcillátor is létrehozható. Szűrőként gyakorlatban csak véges fokszám implementálható. |
| Ugyanolyan meredekséghez tartozó késleltetőszám: több | kevesebb a rekurzió miatt |
| Története: nincs analóg megfelelője, sokfázisú (polyphase) analóg hálózatokkal közelíthető ez az elv. | Analóg szűrők működési elvéből származtatható a működési elve. |
Hogyan néz ki egy ilyen áramkör a gyakorlatban?
Alább két igen elterjedt és mint látható lesz, igen egyszerű megoldás lesz ismertetve. A bonyolultságát a tervezés során az erősítők együtthatóinak meghatározása jelenti. Ez dönti el ugyanis, hogy az adott X késleltetőt tartalmazó FIR vagy IIR szűrő valójában hogyan fog viselkedni.
Elöljáróban annyit megemlítve, hogy az áramkör leges leg elejére A/D átalakítót, a végére D/A átalakítót és aluláteresztő szűrőt téve, az egész rendszer bemenete analóg, a kimenete szintén analóg lesz.
Implementáció digitális logikai IC-kkel
Ahogy a fenti ábrán látható, az összeadó egy bináris összeadó, a szorzó egy bináris szorzó, a késleltető pedig például egy 74HC374-es digitális tároló IC. Mindezt ha egyetlen tokban szeretnénk implementálni, az FPGA, mint tetszőleges sorrendbe konfigurálható logikai kapukat tartalmazó ideális erre a célra.
Implementáció mikrovezérlővel illetve DSP-vel
A fenti rajzon látható logikát követve valósítható meg. A mostani bemenő minta és az előző eltárolt mintákból álló vektort szorozzuk össze a szorzók együtthatóinak vektorával, a részeredményeket pedig összegezzük. És FIR szűrő esetén már készen is van a kimenőjel. IIR szűrő esetén természetesen a kimenőjel előző állapotait tartalmazó vektorral szorozzuk össze a szorzók együtthatóinak vektorával és az eredményeit szintén összegezzük a kimenőjellel.
<source lang="c"> /*
FIR szűrő konvolúciót megvalósító részlete
Bemenetek:
m: <konvhossz> hosszú minta vektor
a: <konvhossz> hosszú együttható vektor
Kimenet: a konvolúció eredménye
- /
float konvolval_fir(const float *m, const float *a, int konvhossz) {
int i; float er=0; for (i=0; i<konvhossz; i++) er += m[i] * a[i]; return er;
} </source>
És nézzünk egy példát az IIR implementációra, ahol mint a fenti blokkvázlaton látható, nem csak az új minták, hanem a régebbi eredmények is meghatározzák az új eredményt.
<source lang="c"> /*
IIR szűrő konvolúciót megvalósító részlete
Bemenetek:
m: <konvhossz> hosszú minta vektor
a: <konvhossz> hosszú együttható vektor
eredm: <konvhossz> hosszú előző eredményekből álló vektor
b: <konvhossz> hosszú együttható vektor a visszacsatoláshoz
Kimenet: a konvolúció eredménye
A kimenetet ne felejtsük el a főprogramban az eredm vektorhoz hozzáilleszteni,
hiszen az alábbi szűrő esetén felhasználjuk a következő számításhoz.
- /
float konvolval_iir(float short *m, const float *a, const float *eredm, const float *b, int konvhossz) {
int i; float er=0; for (i=0; i<konvhossz; i++) er += m[i] * a[i] + eredm[i] * b[i]; return er;
} </source>
És hogy pontosan milyen feladatot lát el a szűrő, azt teljes mértékben az a illetve IIR elrendezés esetén az a és b vektorokban szereplő számértékek határozzák meg. Ezeknek az együtthatóknak a kiszámítására mi is vállalkozhatunk, azonban rengeteg program található az interneten, amely megadja nekünk a szükséges együtthatókat.
További érdekessége az implementációnak, hogy a törtszámok tárolására alkalmas float helyett gyakran olyan kisprocesszort alkalmazunk, amely sokkal gyorsabban képes egész (integer) értékekkel dolgozni. Ebben az esetben a fenti algoritmusokat célszerű úgy átdolgozni, hogy egész számokkal tudjon dolgozni.
A DSP-kben történő implementáláskor pedig számos, az adott architektúra által biztosított gyorsításra van lehetőségünk. Akár a hardveresen határolt ciklikus pufferek, akár a hosszabb eredmény tároló regiszterek (akkumulátorok), akár az egyidejűleg több szálon történő szorzást vagy szorzás+összegzés elemi műveletét nézzük.
Együtthatók meghatározása
- interneten található sok-sok szűrőtervező program valamelyikével
- saját magunk is meghatározhatunk együtthatókat az impulzusválaszából, vagy a Fourier transzformáltból.