„Konvolúció” változatai közötti eltérés
a (→Példák) |
(→Példák) |
||
| 23. sor: | 23. sor: | ||
Nézzünk két egyszerű példát a konvolúció műveletére. | Nézzünk két egyszerű példát a konvolúció műveletére. | ||
| − | + | A bemeneti jelnek (''g'') vegyünk egy feszültségugrást az n=1 időpillanatban: | |
{| border="1" | {| border="1" | ||
| − | | n || 1 || 2 || 3 || 4 | + | | n || 0 || 1 || 2 || 3 || 4 |
|- | |- | ||
| − | | | + | | g(n) || 0 || 1 || 1 || 1 || 1 |
|} | |} | ||
| + | n<0 esetén g(n)=0, n>4 esetén pedig g(n)=1. | ||
| − | + | Az első példában legyenek az ''f'' értékei: | |
{| border="1" | {| border="1" | ||
| − | | | + | | n || 0 || 1 || 2 || 3 || 4 |
|- | |- | ||
| − | | | + | | f(n) || 0 || -1 || 0 || 0 || 0 |
|} | |} | ||
| + | n<0 és n>4 esetén f(n)=0. | ||
| + | A kimeneti jel (h=f*g) értékeit a következőképpen kapjuk: | ||
| + | * h(0) = f(0) g(0) + f(1) g(-1) + f(2) g(-2) + f(3) g(-3) + f(4) g(-4) = 0 | ||
| + | * h(1) = f(0) g(1) + f(1) g(0) + f(2) g(-1) + f(3) g(-2) + f(4) g(-3) = 0 | ||
| + | * h(2) = f(0) g(2) + '''f(1) g(1)''' + f(2) g(0) + f(3) g(-1) + f(4) g(-2) = -1 | ||
| + | * h(3) = f(0) g(3) + '''f(1) g(2)''' + f(2) g(1) + f(3) g(0) + f(4) g(-1) = -1 | ||
| + | * h(4) = f(0) g(4) + '''f(1) g(3)''' + f(2) g(2) + f(3) g(1) + f(4) g(0) = -1 | ||
| + | |||
| + | Dőlttel azok a tagok vannak kiemelve, ahonnan nullától eltérő érték származik az összegbe. | ||
| + | |||
| + | Az eredmény tehát: | ||
| + | {| border="1" | ||
| + | | n || 0 || 1 || 2 || 3 || 4 | ||
| + | |- | ||
| + | | h(n) || 0 || 0 || -1 || -1 || -1 | ||
| + | |} | ||
| + | |||
| + | A kimeneti jelsorozat ebben a példában a bemeneti jel egy időegységgel késleltetett és fázisfordított változata. Ezt az alábbi ábrán lehet szemléltetni (az egyszerűség kedvéért folytonos vonallal ábrázolva a diszkrét értékeket és a két függvényt függőlegesen eltolva): | ||
<gnuplot> | <gnuplot> | ||
| 48. sor: | 67. sor: | ||
set ytics 1 | set ytics 1 | ||
u(n,x) = (x<n ? 0 : (x>=n+1 ? 0 : 1)) | u(n,x) = (x<n ? 0 : (x>=n+1 ? 0 : 1)) | ||
| − | + | g(x) = u(1,x)+u(2,x)+u(3,x)+u(4,x) | |
| − | h(x) = -u(3,x) | + | h(x) = -u(2,x)-u(3,x)-u(4,x) |
| − | plot [0. | + | plot [-0.2:4.8] 2+g(x) w l linewidth 3 title "g", h(x) w l linewidth 3 title "h",0 notitle, 2 notitle |
| + | </gnuplot> | ||
| + | |||
| + | Az második példához már kicsit összetettebb ''f'' függvényt választunk: | ||
| + | {| border="1" | ||
| + | | n || 0 || 1 || 2 || 3 || 4 | ||
| + | |- | ||
| + | | f(n) || 0.6 || 0.3 || 0.1 || 0 || 0 | ||
| + | |} | ||
| + | n<0 és n>4 esetén f(n)=0. | ||
| + | |||
| + | A kimeneti jel (h=f*g) értékeit a következőképpen kapjuk: | ||
| + | * h(0) = f(0) g(0) + f(1) g(-1) + f(2) g(-2) + f(3) g(-3) + f(4) g(-4) = 0 | ||
| + | * h(1) = '''f(0) g(1)''' + f(1) g(0) + f(2) g(-1) + f(3) g(-2) + f(4) g(-3) = 0.6 | ||
| + | * h(2) = '''f(0) g(2)''' + '''f(1) g(1)''' + f(2) g(0) + f(3) g(-1) + f(4) g(-2) = 0.9 | ||
| + | * h(3) = '''f(0) g(3)''' + '''f(1) g(2)''' + '''f(2) g(1)''' + f(3) g(0) + f(4) g(-1) = 1 | ||
| + | * h(4) = '''f(0) g(4)''' + '''f(1) g(3)''' + '''f(2) g(2)''' + f(3) g(1) + f(4) g(0) = 1 | ||
| + | |||
| + | Most az eredmény: | ||
| + | {| border="1" | ||
| + | | n || 0 || 1 || 2 || 3 || 4 | ||
| + | |- | ||
| + | | h(n) || 0 || 0.6 || 0.9 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | <gnuplot> | ||
| + | set output 'konv_pelda2.png' | ||
| + | set grid | ||
| + | set size 0.6, 0.4 | ||
| + | set yrange [-1.5:3.5] | ||
| + | set xlabel "n" | ||
| + | set ylabel "" | ||
| + | set key right 0.5 | ||
| + | set ytics 1 | ||
| + | u(n,x) = (x<n ? 0 : (x>=n+1 ? 0 : 1)) | ||
| + | g(x) = u(1,x)+u(2,x)+u(3,x)+u(4,x) | ||
| + | h(x) = 0.6*u(1,x)+0.9*u(2,x)+u(3,x)+u(4,x) | ||
| + | plot [-0.2:4.8] 2+g(x) w l linewidth 3 title "g", h(x) w l linewidth 3 title "h",0 notitle, 2 notitle | ||
</gnuplot> | </gnuplot> | ||
| + | |||
| + | A minták kicsit száma (5) ellenére látszik, hogy a kimeneti jel lassabban éri el az 1-et, mint | ||
| + | a bementi. A konvolúció ezekkel az együtthatókkal tehát úgy viselkedik, mint egy aluláteresztő szűrő. | ||
| + | |||
| + | Ezzekkel a példákkal egyben a [[FIR]] szűrő működését is illusztráltuk. | ||
== Alkalmazások == | == Alkalmazások == | ||
A lap 2007. június 22., 22:16-kori változata
A konvolúció a jelfeldolgozás egyik legelemibb művelete. Ez a lineáris művelet két függvényből állít elő egy harmadikat. Legegyszerűbben úgy szemléltethető a konvolúció, mint egy adatsorozat (egyik függvényből vett minta) súlyozott mozgó átlagának számítása egy adott súlyfüggvény (a másik függvényből vett minta) alapján.
Tartalomjegyzék
Alapvető tulajdonságok
Az [math]f[/math] és [math]g[/math] függvények konvolúcióját [math]f * g[/math]-vel jelöljük. A „csillag” műveleti jel nem tévesztendő össze a szorzást jelölő ponttal. A hasonlóság azért nem véletlen, mert konvolúció alaptulajonságai megegyeznek a szorzáséval:
- [math]f * g = g * f[/math]
- [math]f * (g + h) = f * g + f * h[/math]
Matematikai leírása
Tekintettel arra, hogy a konvolúció fogalmával a rádióamatőr gyakorlatban csak diszkrét idejű rendszerekben találkozunk, így a matematikai definícióját is erre korlátozzuk.
Vegyünk egy jelfolyamot, melynek pillanatértékei g(m) pontokból állnak. Továbbá egy áramköri egységet, amely a konvolúciót elvégzi. Ennek az áramköri egységnek a konvolúció elvégzéséhez f(1)...f(n) konstans együtthatók állnak rendelkezésre. Ekkor a konvolúció leírható az alábbiak szerint:
- [math](f * g)(m) = \sum_n {f(n) \cdot g(m - n)} \,[/math]
ahol:
- g (mint gerjesztés): a beérkező jel mintái, az elemi mintákat g(m) jelöli.
- f: belső függvény, f(1) ... f(n)-nel jelölve a „mintáit”, tehát egy n hosszú konstans vektor (--> ezt határozza meg az eszköz funkcióját - lásd később).
- f * g: a konvolúció eredménye, (f * g)(m) az eredményül kapott elemi mintákat jelöli
Példák
Nézzünk két egyszerű példát a konvolúció műveletére.
A bemeneti jelnek (g) vegyünk egy feszültségugrást az n=1 időpillanatban:
| n | 0 | 1 | 2 | 3 | 4 |
| g(n) | 0 | 1 | 1 | 1 | 1 |
n<0 esetén g(n)=0, n>4 esetén pedig g(n)=1.
Az első példában legyenek az f értékei:
| n | 0 | 1 | 2 | 3 | 4 |
| f(n) | 0 | -1 | 0 | 0 | 0 |
n<0 és n>4 esetén f(n)=0.
A kimeneti jel (h=f*g) értékeit a következőképpen kapjuk:
- h(0) = f(0) g(0) + f(1) g(-1) + f(2) g(-2) + f(3) g(-3) + f(4) g(-4) = 0
- h(1) = f(0) g(1) + f(1) g(0) + f(2) g(-1) + f(3) g(-2) + f(4) g(-3) = 0
- h(2) = f(0) g(2) + f(1) g(1) + f(2) g(0) + f(3) g(-1) + f(4) g(-2) = -1
- h(3) = f(0) g(3) + f(1) g(2) + f(2) g(1) + f(3) g(0) + f(4) g(-1) = -1
- h(4) = f(0) g(4) + f(1) g(3) + f(2) g(2) + f(3) g(1) + f(4) g(0) = -1
Dőlttel azok a tagok vannak kiemelve, ahonnan nullától eltérő érték származik az összegbe.
Az eredmény tehát:
| n | 0 | 1 | 2 | 3 | 4 |
| h(n) | 0 | 0 | -1 | -1 | -1 |
A kimeneti jelsorozat ebben a példában a bemeneti jel egy időegységgel késleltetett és fázisfordított változata. Ezt az alábbi ábrán lehet szemléltetni (az egyszerűség kedvéért folytonos vonallal ábrázolva a diszkrét értékeket és a két függvényt függőlegesen eltolva):
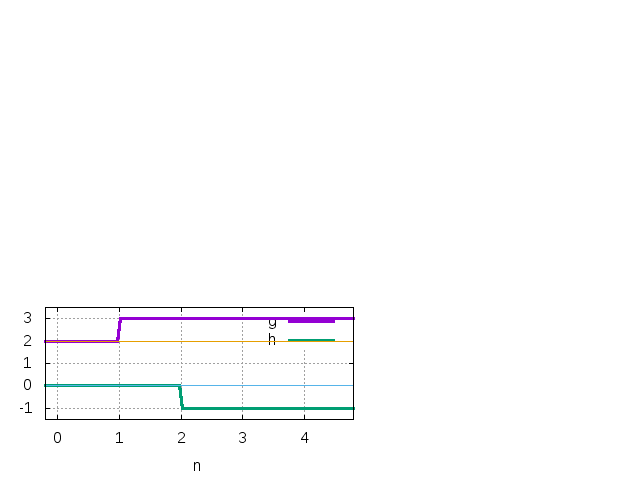
Az második példához már kicsit összetettebb f függvényt választunk:
| n | 0 | 1 | 2 | 3 | 4 |
| f(n) | 0.6 | 0.3 | 0.1 | 0 | 0 |
n<0 és n>4 esetén f(n)=0.
A kimeneti jel (h=f*g) értékeit a következőképpen kapjuk:
- h(0) = f(0) g(0) + f(1) g(-1) + f(2) g(-2) + f(3) g(-3) + f(4) g(-4) = 0
- h(1) = f(0) g(1) + f(1) g(0) + f(2) g(-1) + f(3) g(-2) + f(4) g(-3) = 0.6
- h(2) = f(0) g(2) + f(1) g(1) + f(2) g(0) + f(3) g(-1) + f(4) g(-2) = 0.9
- h(3) = f(0) g(3) + f(1) g(2) + f(2) g(1) + f(3) g(0) + f(4) g(-1) = 1
- h(4) = f(0) g(4) + f(1) g(3) + f(2) g(2) + f(3) g(1) + f(4) g(0) = 1
Most az eredmény:
| n | 0 | 1 | 2 | 3 | 4 |
| h(n) | 0 | 0.6 | 0.9 | 1 | 1 |
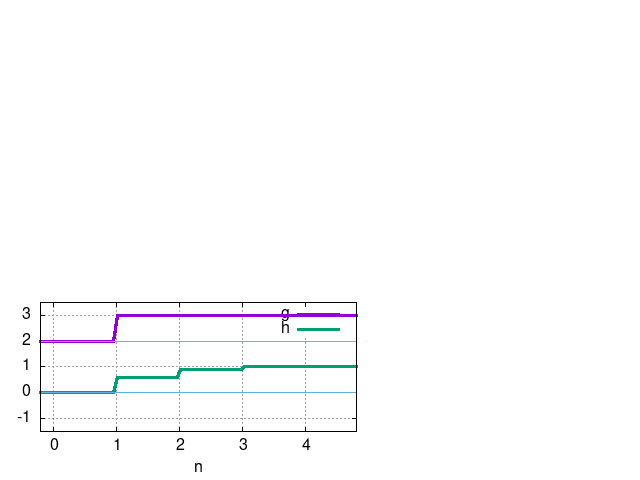
A minták kicsit száma (5) ellenére látszik, hogy a kimeneti jel lassabban éri el az 1-et, mint a bementi. A konvolúció ezekkel az együtthatókkal tehát úgy viselkedik, mint egy aluláteresztő szűrő.
Ezzekkel a példákkal egyben a FIR szűrő működését is illusztráltuk.
Alkalmazások
Diszkrét idejű jelfeldolgozás terén
A konvolúció leg elterjedtebb alkalmazása a digitális szűrőkben található. Megfelelő konstans vektor alkalmazásával érjük el a különböző karakterisztikákat. A konstansok kiszámításához az interneten jobbnál-jobb szűrőtervező szoftverek találhatók. Az algoritmus implementálható jelfeldolgozó processzorokban és mikrovezérlőkben is, de nagysebességű jelfeldolgozás vagy egyéb praktikus szempontok esetén gyakran implementálják FPGA-ban is. Gyengébb minőséget megkövetelő esetben akár nagyobb CPLD-ben is.
Processzoros áramkörben (mikrovezérlő, DSP, személyi számítógép) történő implementálásnál nagy előny, ha a processzor gyors szorzóáramkörrel rendelkezik illetve az is előny, ha hardverből támogatja a ciklikus puffereket. Ezáltal sokkal kevesebb órajel „elpazarlásával” végezhető el a művelet, vagy másszóval sokkal több minta feldolgozható ugyanakkora órajellel járó processzort tartalmazó áramkörrel.
- A szűrőelrendezéseket csoportosítása
- bemenetek száma szerint egy vagy több bemenettel rendelkező
- kimenetek száma szerint egy vagy több kimenettel rendelkező
Alapból az egyetlen bemenettel és egyetlen kimenettel rendelkező szűrőkkel foglalkozunk, ezekből az alappéldákból levezethetőek a több bemenetű illetve több kimenetű elrendezések.
- Elemi szűrőimplementációk
- FIR szűrő (Finite Impulse Response) - véges impulzusválaszú szűrő
- IIR szűrő (Infinite Impulse Response) - végtelen impulzusválaszú szűrő (Butterworth, Chebishev, Cauer szűrők)
- Mi valósítható meg velük?
- Aluláteresztő szűrő (LP filter)
- Felüláteresztő szűrő (HP filter)
- Sáváteresztő szűrő (BP filter)
- Sávzáró szűrő (Notch filter)
- Fázistoló (Delay)
- Hilbert transzformátor (fontos szerepe van az SSB jel demodulásánál)
- Rezonátor (IIR elrendezés megfelelő együtthatók esetén történő gerjedését használja ki)
Egy speciális, úgynevezett átlapolt összeadásos konvolúció az FFT (gyors Fourier transzformáció) eljárás is, amely szintén a legfontosabb jelfeldolgozó algoritmusok egyike. Segítségével apró frekvenciatartományonként vizsgálható az amplitudó és fázis a vizsgált mintában, illetve az elemi amplitudók és fázisok tetszőleges módosítása után a Fourier transzformált jelet visszalakakítva jellé, tetszőleges jelet előállíthatunk a bemenőjelből.
Kétállapotú értékkészlet esetén
Érdemes megemlékezni egy másik igen fontos alkalmazási területről is, ahol a sokbites, finom (analógot reprezentáló) értékkészlet helyett kétállapotú (bináris) formáját használjuk a jelnek. Ilyen bináris alkalmazások a konvolúciós hibajavító eljárások.