Jósági tényező
Tartalomjegyzék
Mi a jósági tényező
Rezgőkörök és rezgőkörrel modellezhető alkatrészek jellemzője a jósági tényező, jele Q. A jósági tényezőt rezonanciafrekvencián szokták számolni. A jósági tényező megadja, hogy mennyivel nagyobb az aránya a képzetes teljesítménynek a valós, eldisszipált teljesítményhez képest.
Párhuzamos rezgőkör jósági tényezőjének számítása
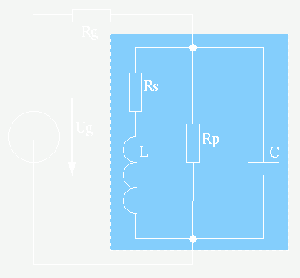
Képzeljünk el egy gyakorlatban megépített párhuzamos RC kört. Ebben található egy tekercs, egy kondenzátor. Továbbá sajnos jelen van a tekercs rézhuzaljának a soros ellenállása (Rs) is.
Mint a Thomson-képletből tudjuk, [math]f_0 = \frac{1}{2\pi\sqrt{LC}}[/math]. Erre a frekvenciára a Q jósági tényező kiszámítható:
[math]Q = \frac{X_L}{R_s} = \frac{2\pi L}{R_s}[/math]
Ugyanakkor ha eljátszunk a gondolattal, és az Rp párhuzamos ellenállásra próbáljuk kiszámítani a jósági tényezőt, nem számítva most az Rs soros ellenállást, akkor
[math]Q = \frac{R_p}{X_L} = \frac{R_p}{2\pi L}[/math]
Ha az eredőjére vagyunk kíváncsiak a külön-külön számolt soros és párhuzamos rezgőkörök által meghatározott jósági tényezőknek, elegendő arra gondolni, hogy a párhuzamos ellenállások repluszolódva adják az eredőjüket. Azaz [math]Q = \frac{Q_s \cdot Q_p}{Q_s + Q_p}[/math].
Sávszélesség kapcsolata a jósági tényezővel
Sávszélesség a 3 dB-lel kisebb feszültségű pontok között: [math]B = \frac{f_0}{Q}[/math], azaz minél nagyobb a jósági tényező, annál keskenyebb szűrőt készíthetünk az áramkörünkkel.
Következményei párhuzamos rezgőkör esetén
A valódi Rs soros ellenállás hatását egy rezgőkör esetén át lehet számolni párhuzamos ellenállássá. A fenti két egyenlet átrendezéséből kijön, hogy a párhuzamos ellenállás. Azaz:
[math]Q = \frac{X_L}{R_s} = \frac{R_p}{X_L}[/math]. Ezt átrendezve [math]R_p = \frac{{X_L}^2}{R_s}[/math]
Hogy miért jó ez? Mert segítségével megmondható, mekkora lesz a párhuzamos ellenállása egy rezonanciafrekvencián rezgő rezgőkörnek. Ebből rögtön kiszámítható a rezonanciafrekvencián várható feszültség.
Következményei soros rezgőkör esetén
Soros rezgőkörnél a Q szintén a fentiek szerint határozható meg. Azt kell tudni a soros rezgőkörről, hogy rezonanciafrekvencián külön-külön nézve a tekercs és a kondenzátor kapcsain ellentétes fázisban, de nagyobb feszültséget mérhetünk, mint a soros RLC körre kívülről rákapcsolt feszültség. Hogy mennyit, az a jósági tényezővel egyenesen arányos.
[math]U_L = U_g \cdot \frac{X_L}{R_s} = U_g \cdot Q[/math]
Ez ténylegesen így működik. Ha például van egy rezgőkörünk, amely XL-je és XC-je az adott frekvencián 100 ohm, a soros ellenállása 1 ohm és erre az egész RLC áramkör részre rákapcsolunk 1 mV-os feszültséget, akkor a kondenzátoron és a tekercsen 100 mV-os feszültség mérhető (nagyimpedanciás műszerrel), azonban a Kirchhoff huroktörvénye sem sérül, mivel a két 100 mV-os szinuszos feszültség fázisa egymáshoz képest 180 fokot zár be, ezáltal az 1 mV teljes egészében az áramkör soros ellenállására jut.