Állóhullám
Állóhullámmal és annak problémájával a rádióamatőr a rádiófrekvenciás tápvonalak alkalmazása során találkozik. Ennek a jelenségnek a hátterével érdemes közelebbről megismerkedni.
Az alábbi szócikk transzverzális hullámokra szorítkozik. Azaz olyan hullámokra, ahol a hullám amplitudója merőleges a hullám terjedési irányával. Ilyen a tápvonalakban terjedő jel, amely fénysebesség nagyságrendjébe eső sebességgel rohan végig a tápvonalon, az amplitudója (feszültsége) azonban egy terjedési irányra merőleges modellként rajzolható le. A másik ilyen szemléletes és látható példa egy tetszőleges kifeszített húr, amely egyik végét kitérítve a kitérés végigszalad a húron a másik vége felé.
Tartalomjegyzék
Az állóhullám kialakulása
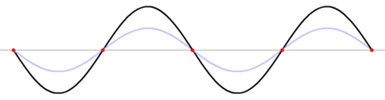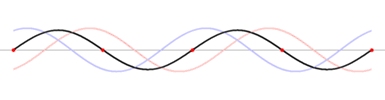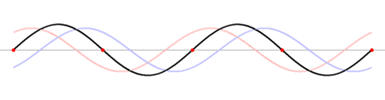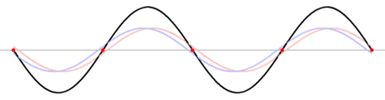
A transzverzális hullámvezető egyik végére szinuszos jelforrást kapcsolva a szinuszjel végigszalad a hullámvezetőn, majd a hullámvezető végén visszaverődik. A visszaverődő jel az folyamatosan érkező gerjesztőjellel együtt hozza létre az ábrán látható állóhullámot.
Miért káros ez?
Több okból sem szerencsés tápvonalakban az állóhullám.
- a haladó hullám mellett a visszaverődő hullám nem a terhelésre jut, hanem a tápvonalat melegíti.
- a duzzadópontokon a feszültség a normál üzemi feszültség többszöröse, amely feszültség hatására tönkremehet a végfok tranzisztor.
- a kábel „lengése” többlet kisugárzással jár, amely zavarhatja az épületben levő egyéb elektronikai berendezéseket.
Az állóhullám kimutatása
Kísérleti úton
Az állóhullám közvetlenül kimutatható. Például egy szigeteletlen szimmetrikus tápvonalon végighúzott feszültségindikátor látványosan kimutatja a duzzadópontokat.
Ha tágabb frekvenciatartományban képes üzemelni a rendszerünk, és ez a frekvenciatartomány az alkalmazott kábelhosszra kivetítve több mint fél hullámhossznyi különbséget lefed, akkor érdekes kísérlet végezhető el. Az alábbi részben ismertetett feszültségosztó kapcsolás segítségével azt tapasztalhatjuk, hogy a frekvencia állításával az Uki bizonyos frekvenciákon magas, bizonyos frekvenciákon alacsony értéket vesz fel, attól függően hogy a kábelhossz az adott frekvenciára λ/2 egész számú többszöröse vagy az előbbi λ/4-gyel való eltoltja.
Megjegyzés: ez utóbbi mérési elrendezéssel egyébként a kábel paraméterei (rövidülési tényező, kábelveszteség) is jól kimérhetőek, ha a kábelvéget rövidzárral vagy szabadonhagyva szakadással zárjuk. Öreg kábeleink paramétereit lehet vele ellenőrizni.
Számítással
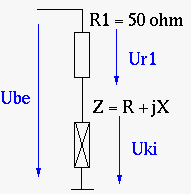
Azonban a gyakorlatban a kábel szakaszaihoz való közvetlen hozzáférés helyett inkább a bemeneti paraméterekből számítjuk. A számítás alapja a tápvonal meghajtásánál a tápvonal bemenőimpedanciájának (Z = R + jX) névleges impedanciától való eltérése. Ez kimutatható például egy feszültségosztó kapcsolással, ahol a felső tag egy névleges impedanciát képviselő ellenállás, az alsó tag maga a tápvonal. Ekkor a meghajtó feszültség és a két alkatrészen mérhető feszültség csúcsértékeiből kiszámítható. Ha ez eltér az üzemi frekvencián névleges impedanciától, akkor állóhullám fog benne kialakulni.
- A kiszámítás matematikai háttere
[math]U_{ki} = U_{be}\cdot\frac{Z}{R_1 + Z} = U_{be}\cdot\frac{R + jX}{R_1 + R + jX}[/math]
Ám ha maximális feszültégértkekkel számolunk, mert diódával + szűrőkondenzátorral a csúcsfeszültséget indikáljuk, akkor 3 mérési eredményhez jutunk:
[math]\hat U_{be} = \sqrt{2} \cdot U_{be}[/math]
[math]\hat U_{ki} = \sqrt{2} \cdot U_{ki}[/math]
[math]\hat U_{r1} = \sqrt{2} \cdot U_{r1}[/math]
<szamolo sor=10 oszlop=25 jobb szoveg="A három, akár csúcsegyenirányított feszültségből\\a terhelés R és X paraméterei számolható ki.">Ube = 2,8;Ur1 = 1,5;Uki = 1,7;R1 = 50;;Zabs=Uki/Ur1*R1;szog=acos((Ube-Ur1)/Uki);;R=Zabs*cos(szog);X=Zabs*sin(szog)</szamolo>
Azonban a fázisszöget ebből nem látjuk. Viszont azt tudjuk, hogy az elemi komponensek feszültségeinek összege kiadja a bemenőfeszültséget. Komplex értékként az abszolutértékek fázisszögével.
[math]\hat U_{be} = \hat U_{r1} + cos(\varphi) \cdot \hat U_{ki}[/math]
Ebből meghatározható a fázisszög. Továbbá azt is belátható, hogy az Ur1 és Uki értékenek aránya arányos az impedancia abszolutértékeinek arányával:
[math]\frac{\hat U_{ki}}{\hat U_{r1}} = \frac{|Z|}{R_1}[/math]
Ebből az R és X értékei: [math]R = |Z| \cdot cos(\varphi)[/math] és [math]X = |Z| \cdot sin(\varphi)[/math]
A leírt összefüggésekből már kiszámítható az R és X paraméter. Egy további méréssel pedig az X előjele is (kapacitív vagy induktív) meghatározható.
Hogyan csökkenthető vagy szüntethető meg az állóhullám?
Ha a tápvonal végén hullámtanilag ugyanolyan paraméterű „közeget” érez, akkor a hullám teljes energiája továbbhalad ebbe a további részbe. Amennyiben eltér a hullámtani paramétere a folytatásnak, akkor az eltérés függvényében az energia egy része visszaverődik. A feladat tehát egy olyan terhelőimpedancia (Z = R + jX) biztosítása, amely megegyezik a tápvonal hullámimpedanciájával.